题目内容
6. 在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )
在第15届机器人世界杯赛上,中科大“蓝鹰”队获得仿真2D组冠军和服务机器人组亚军.如图所示,科大著名服务机器人“可佳”要执行一项任务,给它设定了如下动作程序:在平面内由点(0,0)出发,沿直线运动到点(3,1),再由点(3,1)沿直线运动到点(1,4),又由点(1,4)沿直线运动到点(5,5),然后由点(5,5)沿直线运动到点(2,2).该个过程中机器人所用时间是2$\sqrt{2}$s,则( )| A. | 机器人的运动轨迹是一条直线 | |
| B. | 机器人不会两次通过同一点 | |
| C. | 整个过程中机器人的位移大小为$\sqrt{2}$m | |
| D. | 整个过程中机器人的平均速度为1.0m/s |
分析 依据坐标位置的变化可表示位移和路程,平均速率为路程与时间的比值,平均速度为位移与时间的比值.
解答 解:A、由题目给定的坐标位置变化可知机器人的运动轨迹为折线,A错误;
B、由点(5,5)沿直线运动到点(2,2)时会与由点(3,1 )沿直线运动到点(1,4)有交点,即会经过同一位置,B错误;
C、由题意知机器人初位置坐标为(0,0),末位置坐标为(2.2),故位移为:X=$\sqrt{{2}^{2}+{2}^{2}}m=2\sqrt{2}m$,故C错误.
D、平均速度$\overline{v}$=$\frac{X}{t}$=$\frac{2\sqrt{2}}{2\sqrt{2}}$=1m/s;故D正确;
故选:D.
点评 本题考查了位移与平均速度的求解方法,注意平均速度的大小等于位移与时间的比值.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
17. 在匀强磁场中,一矩形金属线圈绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线圈绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
 在匀强磁场中,一矩形金属线圈绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )
在匀强磁场中,一矩形金属线圈绕与磁感线垂直的转轴匀速转动,如图甲所示,产生的交变电动势的图象如图乙所示,则( )| A. | t=0.005s时线圈平面与磁场方向平行 | |
| B. | t=0.01s时线圈的磁通量变化率最大 | |
| C. | 线圈产生的交变电动势频率为50Hz | |
| D. | 线圈产生的交变电动势有效值为311 V |
14. 如图所示,质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h.若以小球释放的初始位置为参考平面,那么,小球落地时的机械能及整个过程中重力势能的变化分别是( )
如图所示,质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h.若以小球释放的初始位置为参考平面,那么,小球落地时的机械能及整个过程中重力势能的变化分别是( )
 如图所示,质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h.若以小球释放的初始位置为参考平面,那么,小球落地时的机械能及整个过程中重力势能的变化分别是( )
如图所示,质量为m的小球,从离桌面H高处由静止下落,桌面离地高度为h.若以小球释放的初始位置为参考平面,那么,小球落地时的机械能及整个过程中重力势能的变化分别是( )| A. | 0,减少mg(H-h) | B. | 0,减少mg(H+h) | C. | mgh,减少mg(H-h) | D. | mgH,减少mg(H+h) |
11. 质量之比2:1的球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内,细线承受的拉力为F;某时刻突然剪断细线,则在细线断的瞬间A、B球的加速度分别为( )
质量之比2:1的球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内,细线承受的拉力为F;某时刻突然剪断细线,则在细线断的瞬间A、B球的加速度分别为( )
 质量之比2:1的球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内,细线承受的拉力为F;某时刻突然剪断细线,则在细线断的瞬间A、B球的加速度分别为( )
质量之比2:1的球A、B,由轻质弹簧相连后再用细线悬挂在正在竖直向上做匀速运动的电梯内,细线承受的拉力为F;某时刻突然剪断细线,则在细线断的瞬间A、B球的加速度分别为( )| A. | aA=g,aB=g | B. | aA=0,aB=0.5g | C. | aA=1.5g,aB=0 | D. | aA=0.5g,aB=1.5g |
18. 一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该 水平面上做半径为r的圆周运动,设质点的最初速率是v0,滑动摩擦力大小恒定,当它运动一周时,其速率变为$\frac{{v}_{0}}{2}$,则( )
一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该 水平面上做半径为r的圆周运动,设质点的最初速率是v0,滑动摩擦力大小恒定,当它运动一周时,其速率变为$\frac{{v}_{0}}{2}$,则( )
 一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该 水平面上做半径为r的圆周运动,设质点的最初速率是v0,滑动摩擦力大小恒定,当它运动一周时,其速率变为$\frac{{v}_{0}}{2}$,则( )
一质量为m的质点,系在轻绳的一端,绳的另一端固定在水平面上,水平面粗糙.此质点在该 水平面上做半径为r的圆周运动,设质点的最初速率是v0,滑动摩擦力大小恒定,当它运动一周时,其速率变为$\frac{{v}_{0}}{2}$,则( )| A. | 当它运动一周时摩擦力做的功为-$\frac{3}{8}$mv${\;}_{0}^{2}$ | |
| B. | 质点与水平面的动摩擦因数为μ=$\frac{3{v}_{0}^{2}}{16πrg}$ | |
| C. | 质点在运动了两个周期时恰好停止 | |
| D. | 当质点运动一周时的向心加速度大小为$\frac{{v}_{0}^{2}}{4r}$ |
15. 如图所示的实验装置中,平行板电容器两极板的正对面积为S,两极板的间距为d,电容器所带电荷量为Q,电容为C,静电计指针的偏转角为α,平行板中间悬挂了一个带电小球,悬线与竖直方向的夹角为θ,下列说法正确的是( )
如图所示的实验装置中,平行板电容器两极板的正对面积为S,两极板的间距为d,电容器所带电荷量为Q,电容为C,静电计指针的偏转角为α,平行板中间悬挂了一个带电小球,悬线与竖直方向的夹角为θ,下列说法正确的是( )
 如图所示的实验装置中,平行板电容器两极板的正对面积为S,两极板的间距为d,电容器所带电荷量为Q,电容为C,静电计指针的偏转角为α,平行板中间悬挂了一个带电小球,悬线与竖直方向的夹角为θ,下列说法正确的是( )
如图所示的实验装置中,平行板电容器两极板的正对面积为S,两极板的间距为d,电容器所带电荷量为Q,电容为C,静电计指针的偏转角为α,平行板中间悬挂了一个带电小球,悬线与竖直方向的夹角为θ,下列说法正确的是( )| A. | 若增大d,则α增大,θ不变 | |
| B. | 若增大d,则α减小,θ不变 | |
| C. | 将A板向上提一些时,α增大,θ增大 | |
| D. | 在两板间插入云母片时,则α减小,θ不变 |
16. 如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )
如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )
 如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )
如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )| A. | 木块A对木块B的摩擦力方向向右 | B. | 木块B对木块C的摩擦力方向向右 | ||
| C. | 木块A对木块C的摩擦力方向向右 | D. | 木块C对木块B的摩擦力方向向右 |
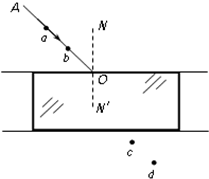 如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面的法线NN′,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针a、b,透过玻璃砖观察大头针a、b的像,在c位置插的大头针正好挡住a、b的像,在d位置插的大头针正好挡住前三个大头针的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出角i和角r.
如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面的法线NN′,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针a、b,透过玻璃砖观察大头针a、b的像,在c位置插的大头针正好挡住a、b的像,在d位置插的大头针正好挡住前三个大头针的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出角i和角r. 如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?
如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?