题目内容
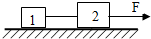 如图所示,放在水平地面上的1、2两木块用轻质短钩相连,质量分别为m1=1.0kg和m2=2.0kg,与地面之间的滑动摩擦系数均为μ=0.1.在t=0s时开始用向右的水平恒力F=6.0N拉木块2,运动一段时间后短钩脱开,到t=6s时,1、2两木块相距S=8.0m,而木块1早已停住了,那么此时木块2的速度是多大?
如图所示,放在水平地面上的1、2两木块用轻质短钩相连,质量分别为m1=1.0kg和m2=2.0kg,与地面之间的滑动摩擦系数均为μ=0.1.在t=0s时开始用向右的水平恒力F=6.0N拉木块2,运动一段时间后短钩脱开,到t=6s时,1、2两木块相距S=8.0m,而木块1早已停住了,那么此时木块2的速度是多大?(已知取g=10m/s2,取
| 368 |
分析:先假设脱钩前两木块一起运动时间为t1,对整体,根据动量定理列式得到脱钩时两木块的速度v1的表达式.脱钩后,根据动能定理分别对两个物体列式,并对拉钩后木块2的运动过程,运用动量定理列式,结合两木块路程的关系,即可求解.
解答:解:设脱钩前两木块一起运动时间为t1,脱钩时两木块的速度为V1,根据题意如下,对两木块脱钩前过程,运用动量定理有
[F-μ(m1+m2)g]t1=(m1+m2)v1
对脱钩后的木块1运用动能定理有-μm1gS1=0-
m1
对脱钩后的木块2运用动能定理有 (F-μm2g)S2=
m2
-
m1
同时,对脱钩后的木块2运用动量定理有 (F-μm2g)(6-t1)=m2v2-m2v1
并运用两木块路程的几何关系有S2-S1=S
联立以上分析式可以算出v2=8.4m/s(另一根V2=27.6m/s舍去了).
答:此时木块2的速度是8.4m/s.
[F-μ(m1+m2)g]t1=(m1+m2)v1
对脱钩后的木块1运用动能定理有-μm1gS1=0-
| 1 |
| 2 |
| v | 2 1 |
对脱钩后的木块2运用动能定理有 (F-μm2g)S2=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 1 |
同时,对脱钩后的木块2运用动量定理有 (F-μm2g)(6-t1)=m2v2-m2v1
并运用两木块路程的几何关系有S2-S1=S
联立以上分析式可以算出v2=8.4m/s(另一根V2=27.6m/s舍去了).
答:此时木块2的速度是8.4m/s.
点评:本题运用动量定理、动能定理研究脱钩问题,也可以根据牛顿第二定律、运动学公式进行求解.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 滑块C离开A时的速度VC’
滑块C离开A时的速度VC’