题目内容
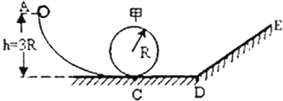
【题目】如图所示半径为R的光滑圆形轨道甲，固定在一竖直平面内，它的左右侧分别为光滑的圆弧形轨道AC和光滑斜面轨道DE，斜面DE与水平轨道CD间衔接良好，无能量损失，CD是一条水平轨道，小球与CD段间的动摩擦因数为μ．若小球从离地3R的高处A点由静止自由释放，可以滑过甲轨道，经过CD段又滑上光滑斜面．求
（1）小球经过甲圆形轨道的最高点时小球的速度大小；
（2）为使球到达光滑斜面后返回时，能通过甲轨道，问CD段的长度不超过多少？
【答案】（1）
；（2）
．
【解析】（1）设小球通过甲轨道最高点时速度为V1，
由机械能守恒定律得： 
解得：V1=
（2）设小球在甲轨道作圆周运动能通过最高点的最小速度为Vmin，
则： 
得：vmin=
设CD段的长度为L，球从A点下滑，到斜面返回通过甲轨道最高点的过程中，根据动能定律：
解得： 
练习册系列答案
阅读快车系列答案
相关题目
