题目内容
【题目】如图所示，在竖直平面内，水平x轴的上方和下方分别存在方向垂直纸面向外和方向垂直纸面向里的匀强磁场，其中x轴上方的匀强磁场磁感应强度大小为B1，并且在第一象限和第二象限有方向相反，强弱相同的平行于x轴的匀强电场，电场强度大小为E1.已知一质量为m的带电小球从y轴上的A(0，L)位置斜向下与y轴负半轴成60°角射入第一象限，恰能做匀速直线运动.
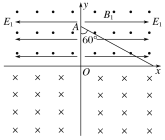
(1)判定带电小球的电性，并求出所带电荷量q及入射的速度大小；
(2)为使得带电小球在x轴下方的磁场中能做匀速圆周运动，需要在x轴下方空间加一匀强电场，试求所加匀强电场的方向和电场强度的大小；
(3)在满足第(2)问的基础上，若在x轴上安装有一绝缘弹性薄板，并且调节x轴下方的磁场强弱，使带电小球恰好与绝缘弹性板碰撞两次后从x轴上的某一位置返回到x轴的上方(带电小球与弹性板碰撞时，既无电荷转移，也无能量损失，并且入射方向和反射方向的关系类似光的反射)，然后恰能匀速直线运动至y轴上的A(0，L)位置，求：弹性板的最小长度及带电小球从A位置出发返回至A位置过程中所经历的时间.
【答案】(1)负电 
(2)竖直向下 
E1
(3) 
L 
＋
【解析】(1)
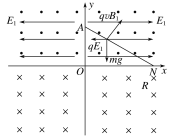
小球在第一象限中的受力分析如图所示，所以带电小球的电性为负电
mg＝qE1tan60°
q＝
又qE1＝qvB1cos60°
即v＝
(2)小球若在x轴下方的磁场中做匀速圆周运动，必须使得电场力与重力二力平衡，即应施加一竖直向下的匀强电场，
且电场强度大小满足：qE＝mg
即E＝E1
(3)要想让小球恰好与弹性板发生两次碰撞，并且碰撞后返回x轴上方空间匀速运动到A点，则其轨迹应该如图所示，
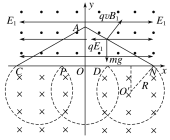
且由几何关系可知：
3PD＝2ON
＝
＝tan60°
联立上述方程解得：
PD＝DN＝
L
则挡板长度至少为PD＝L
设在x轴下方的磁场磁感应强度为B，则满足：
qvB＝m
T＝
从N点运动到C点的时间为：
t＝3×T
联立上式解得：t＝
由几何关系可知：
＝cos60°
在第一象限运动的时间t1和第二象限中运动的时间t2相等，且：
t1＝t2＝
＝
＝
所以带电小球从A点出发至回到A点的过程中所经历的总时间为：
t0＝t＋t1＋t2
联立上述方程解得：t0＝＋
