题目内容
4.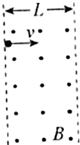 如图所示,一带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s,沿着垂直于磁场方向,且垂直于磁场边界的方向射入匀强磁场中,已知磁场强度B=0.17T,磁场的宽度L=10cm,取g=10m/s2.
如图所示,一带电粒子的质量m=1.7×10-27kg,电荷量q=1.6×10-19C,以速度v=3.2×106m/s,沿着垂直于磁场方向,且垂直于磁场边界的方向射入匀强磁场中,已知磁场强度B=0.17T,磁场的宽度L=10cm,取g=10m/s2.(1)带电粒子离开磁场时速度为多大?
(2)速度方向与入射方向之间的偏折角为多大?
(3)带电粒子在磁场中运动的时间为多长?
(4)离开磁场时偏离入射方向的距离为多大?
分析 (1)带电粒子在匀强磁场中做匀速圆周运动,故粒子离开磁场速度大小不变;
(2)由提供的数据可解半径数值,结合磁场宽度可解圆心角度数,由几何关系可得偏转角,
(3)由洛伦兹力提供向心力求得周期公式,由运动径迹得到圆弧运动时间与周期的关系,进而求出时
(4)由几何知识求出粒子离开磁场时的偏移量.
解答 解:(1)粒子在磁场中做匀速圆周运动,洛伦兹力不做功,粒子的速度大小不变,粒子离开磁场时的速度大小为:3.2×106m/s;
(2)粒子在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
代入数据解得:r=0.2m=20cm,
由几何知识得:sinθ=$\frac{L}{r}$=$\frac{1}{2}$,
解得:θ=30°,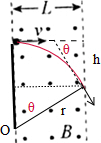
即:带电粒子离开磁场时的偏转角为:θ=30°
(3)带电粒子在磁场中运动的时间为:
t=$\frac{θ}{360°}$T=$\frac{30°}{360°}$×$\frac{2πm}{qB}$,
代入数据解得:t=3.3×10-8s;
(4)根据图示,由几何知识得:
h=r-rcosθ=20-20$\frac{\sqrt{3}}{2}$=(20-10$\sqrt{3}$)cm;
答:(1)带电粒子离开磁场时速度为3.2×106m/s;
(2)速度方向与入射方向之间的偏折角为30°;
(3)带电粒子在磁场中运动的时间为3.3×10-8s;
(4)离开磁场时偏离入射方向的距离为(20-10$\sqrt{3}$)cm.
点评 本题考查带电粒子在磁场中的运动,根据题意作出粒子运动轨迹是正确解题的关键;分析轨迹中的几何关系,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
相关题目
14.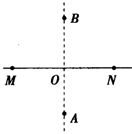 如图所示,在真空中有两个带等量正电的点电荷,分别置于M、N两点,A、B为M、N连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
如图所示,在真空中有两个带等量正电的点电荷,分别置于M、N两点,A、B为M、N连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
 如图所示,在真空中有两个带等量正电的点电荷,分别置于M、N两点,A、B为M、N连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )
如图所示,在真空中有两个带等量正电的点电荷,分别置于M、N两点,A、B为M、N连线的中垂线上的两点,现将一负电荷q由A点沿中垂线移动到B点,在此过程中,下列说法正确的是( )| A. | q的电势能逐渐减少 | B. | q的电势能逐渐增大 | ||
| C. | q的电势能先增大后减小 | D. | q的电势能先减小后增大 |
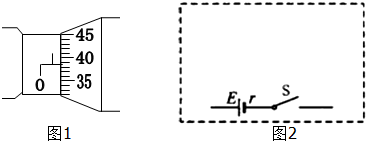
19. 如图所示的电路中,电源内阻r小于电阻R1,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数分别用I、U1、U2和U3表示,电表的示数变化量的大小分别用△I、△U1、△U2和△U3表示,下列有关各绝对值关系式正确的是( )
如图所示的电路中,电源内阻r小于电阻R1,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数分别用I、U1、U2和U3表示,电表的示数变化量的大小分别用△I、△U1、△U2和△U3表示,下列有关各绝对值关系式正确的是( )
 如图所示的电路中,电源内阻r小于电阻R1,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数分别用I、U1、U2和U3表示,电表的示数变化量的大小分别用△I、△U1、△U2和△U3表示,下列有关各绝对值关系式正确的是( )
如图所示的电路中,电源内阻r小于电阻R1,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数分别用I、U1、U2和U3表示,电表的示数变化量的大小分别用△I、△U1、△U2和△U3表示,下列有关各绝对值关系式正确的是( )| A. | $\frac{|△{U}_{1}|}{|△I|}$<$\frac{|△{U}_{2}|}{|△I|}$<$\frac{|△{U}_{3}|}{|△I|}$ | B. | $\frac{|△{U}_{2}|}{|△I|}$<$\frac{|△{U}_{1}|}{|△I|}$<$\frac{|△{U}_{3}|}{|△I|}$ | ||
| C. | $\frac{|△{U}_{3}|}{|△I|}$<$\frac{|△{U}_{2}|}{|△I|}$<$\frac{|△{U}_{1}|}{|△I|}$ | D. | $\frac{|△{U}_{3}|}{|△I|}$<$\frac{|△{U}_{1}|}{|△I|}$<$\frac{|△{U}_{2}|}{|△I|}$ |
9.在平直的公路上,自行车与同方向行驶的一汽车同时经过A点,自行车以V=7m/s的速度做匀速直线运动,汽车以v0=10m/s的速度、a=0.25m/s2的加速度做匀减速直线运动,则自行车追上汽车所用的时间是( )
| A. | 40s | B. | 48s | C. | 50s | D. | 24s |
16.用多用电表欧姆档测电阻,有许多注意事项,下列说法中哪些是错误的( )
| A. | 测量前必须调整定位螺丝,待指针指零,而且每测一次电阻都要重新调零 | |
| B. | 每次换档后必须欧姆调零 | |
| C. | 待测电阻如果是连接在某电路中,应把它与其它元件断开,再进行测量 | |
| D. | 两个表笔要与待测量电阻接触良好才能使测量更准确,为此应当用两个手分别将两个表笔与电阻两端紧紧捏在一起 |
13.一质量为1kg的物体被人用手由静止向上提升1m,这时物体的速度为2m/s,则下列说法中正确的是( )
| A. | 手对物体做功2J | B. | 合外力对物体做功12J | ||
| C. | 合外力对物体做功2J | D. | 物体克服重力做功8J |

 如图所示为通电螺线管的纵剖面图,“?”和“⊙”分别表示导线中的电流垂直纸面流进和流出,图中四个小磁针(涂黑的一端为N极)静止时的指向画法正确的是( )
如图所示为通电螺线管的纵剖面图,“?”和“⊙”分别表示导线中的电流垂直纸面流进和流出,图中四个小磁针(涂黑的一端为N极)静止时的指向画法正确的是( )