题目内容
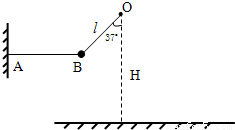
如图所示,O点距水平地面的高度为H=3m,不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球(可视为质点),另一根水平细线一端固定在墙上A点,OB线与竖直方向的夹角为37°,l<lAB,l<H,g取10m/s2,空气阻力不计.(sin37°=0.6,cos37°=0.8)(1)求细线AB与OB上的张力.
(2)若OB的长度l=1m,剪断细线AB的同时,在竖直平面内垂直OB的方向上,给小球一个斜向下的初速度v,为使小球恰好能在竖直平面内做完整的圆周运动,求v的大小
(3)若先剪断细线AB,当小球由静止运动至最低点时再瞬间断开OB,小球最终落地,求OB的长度l为多长时,小球落地点与O点的水平距离最远,最远水平距离是多少.
【答案】分析:(1)对小球受力分析,根据共点力平衡条件,结合平行四边形定则,可求出细线AB与OB上的拉力;
(2)为使小球恰好能在竖直平面内做完整的圆周运动,则小球运动到最高点时最小速度为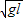 ,即仅仅由重力提供向心力.再由机械能守恒来算出小球的初速度;
,即仅仅由重力提供向心力.再由机械能守恒来算出小球的初速度;
(3)当瞬间断开OB,小球做平抛运动,根据平抛运动的处理规律,结合数学知识,从而确定当长度取何值时,水平距离最远.
解答:解:对小球受力,如图所示:
(1)AB上的张力F1=mgtan37°=15N
OB上的张力F2=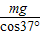 =25N
=25N
(2)小球恰好在竖直平面内做完整的圆周运动,最高点满足仅仅由重力提供向心力,即为 mg=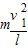
从抛出点到最高点,只有重力做功,小球机械能守恒,
根据机械能守恒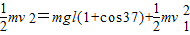
得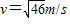
(3)小球由静止运动到最低点过程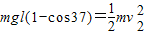
得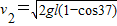
OB线断开后小球做平抛运动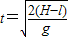
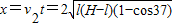
当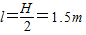
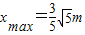
答:(1)求细线AB拉力为15N、OB上的拉力为25N.
(2)为使小球恰好能在竖直平面内做完整的圆周运动,则v的大小为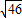 m/s;
m/s;
(3)当瞬间断开OB,小球最终落地,当OB的长度l为1.5m时,小球落地点与O点的水平距离最远,最远水平距离是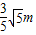 .
.
点评:(1)学会对物体受力分析,并会用平行四边形定则确定力与力的关系;
(2)运用机械能守恒定律,紧扣小球恰好能通过最高点,由重力提供向心力,从而求出此处的速度.
(3)运用动能定理与平抛运动的规律,同时涉及到数学知识:列出长度与水平距离的方程中,当长度取何值时,水平距离最远.
(2)为使小球恰好能在竖直平面内做完整的圆周运动,则小球运动到最高点时最小速度为
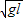 ,即仅仅由重力提供向心力.再由机械能守恒来算出小球的初速度;
,即仅仅由重力提供向心力.再由机械能守恒来算出小球的初速度;(3)当瞬间断开OB,小球做平抛运动,根据平抛运动的处理规律,结合数学知识,从而确定当长度取何值时,水平距离最远.
解答:解:对小球受力,如图所示:
(1)AB上的张力F1=mgtan37°=15N
OB上的张力F2=
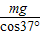 =25N
=25N(2)小球恰好在竖直平面内做完整的圆周运动,最高点满足仅仅由重力提供向心力,即为 mg=
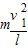
从抛出点到最高点,只有重力做功,小球机械能守恒,
根据机械能守恒
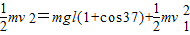
得
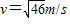
(3)小球由静止运动到最低点过程
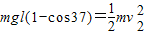
得
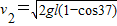
OB线断开后小球做平抛运动
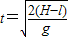
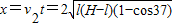
当
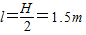
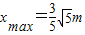
答:(1)求细线AB拉力为15N、OB上的拉力为25N.
(2)为使小球恰好能在竖直平面内做完整的圆周运动,则v的大小为
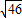 m/s;
m/s;(3)当瞬间断开OB,小球最终落地,当OB的长度l为1.5m时,小球落地点与O点的水平距离最远,最远水平距离是
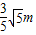 .
.点评:(1)学会对物体受力分析,并会用平行四边形定则确定力与力的关系;
(2)运用机械能守恒定律,紧扣小球恰好能通过最高点,由重力提供向心力,从而求出此处的速度.
(3)运用动能定理与平抛运动的规律,同时涉及到数学知识:列出长度与水平距离的方程中,当长度取何值时,水平距离最远.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
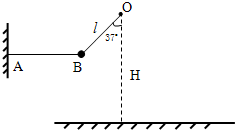 如图所示,O点距水平地面的高度为H=3m,不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球(可视为质点),另一根水平细线一端固定在墙上A点,OB线与竖直方向的夹角为37°,l<lAB,l<H,g取10m/s2,空气阻力不计.(sin37°=0.6,cos37°=0.8)
如图所示,O点距水平地面的高度为H=3m,不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球(可视为质点),另一根水平细线一端固定在墙上A点,OB线与竖直方向的夹角为37°,l<lAB,l<H,g取10m/s2,空气阻力不计.(sin37°=0.6,cos37°=0.8)