��Ŀ����
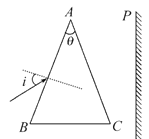
����Ŀ��٤�������о��˶������Ĺ�ϵʱ������������һ����Ħ��������ʵ�飺��ͼ��ʾ����A�㴦����һ��������������B�㴦���֣����ڵ���B�ȸߵ�C����������A�����·���E����һ���ӣ�������˶�·���ᷢ���ı䣬�����������뿪ʼ�ȸߵ�D�������ͼ�еİ��߳�Ϊl����ʼʱ�̰�������ֱ��֮��ļн�Ϊ60�㣬�������ٶ�Ϊg����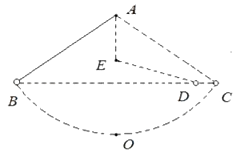
��1������ڵ���͵�Oʱ�ٶȵĴ�С��
��2����E���Ķ������ƣ���������A�ľ������ٶ��ʱ��������º�������ֱ������������Բ���˶���
���𰸡�
��1���⣻�����˶�������Ħ������ֻ��������������ô��е���غ㣻��С�������Ϊm�����У�
mgl��1��cos60�㣩= ![]() ��
��
��ã�v= ![]() ��
��
�𣺰���ڵ���͵�Oʱ�ٶȵĴ�СΪ ![]() ��
��
��2���⣻��С��ǡ��ͨ����ߵ�ʱ�������뾶ΪR������ߵ㴦����ţ�ٵڶ����ɵã�
mg=m ![]() ��
��
����͵㵽��ߵ��ɶ��ܶ����ã���2mgR= ![]() ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
��ã�R= ![]() ��
��
������AE=l�� ![]() =
= ![]() ��
��
�𣺽�E���Ķ������ƣ���������A�ľ�������Ϊ ![]() ʱ��������º�������ֱ������������Բ���˶���
ʱ��������º�������ֱ������������Բ���˶���
����������1������ڵ���͵�����������е���غ�Ů��е���غ�����������͵���ٶȡ�
��2��С��ǡ��ͨ����ߵ������ṩ����������϶��ܶ���������롣
�����㾫�����������⣬������Ҫ�˽�������(����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ��������)����Ҫ���ն��ܶ������ۺ�Ӧ��(Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ��)�����֪ʶ���Ǵ���Ĺؼ���

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�