题目内容
一物体静止在光滑水平面上，先对物体施加一个水平向右的恒力F1，经过时间t物体运动到距离出发点为s的位置，此时立即撤去F1，同时对物体施加一水平向左的恒力F2，又经过相同的时间t，物体运动到距离出发点还有
的位置，在这一过程中力F1和F2的比是（ ）
| s |
| 2 |
分析：开始物体做匀加速运动，后来物体做匀减速运动，由牛顿第二定律求出加速度，然后由位移公式求出速度，最后看看呀求出拉力之比．
解答：解：由牛顿第二定律得：F1=ma1，F2=ma2，
撤去F1时物体的速度v=a1t，
由匀变速运动的位移公式得：
s=
a1t2，-
=vt-
a2t2，
解得：
=
；
故选B．
撤去F1时物体的速度v=a1t，
由匀变速运动的位移公式得：
s=
| 1 |
| 2 |
| s |
| 2 |
| 1 |
| 2 |
解得：
| F1 |
| F2 |
| 2 |
| 5 |
故选B．
点评：知道物体的运动性质，应用牛顿第二定律求出加速度，由速度公式求出物体的速度，由位移公式求出物体的位移即可正确解题，解题时要注意位移的方向．
练习册系列答案
智慧小复习系列答案
相关题目
（2010?长宁区二模）一物体静止在光滑水平面上，同时受到两个方向相反的水平拉力F1、F2的作用，Fl、F2随位移变化，如图所示．则物体的动能将（ ）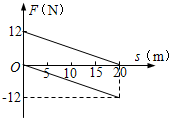
（2006?宜昌模拟）一物体静止在光滑水平面上，同时受到两个水平拉力F1、F2的作用，Fl、F2与位移的关系如图所示，则物体出现动能最大值时物体发生的位移大小应为（ ）