题目内容
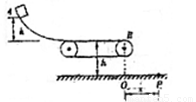
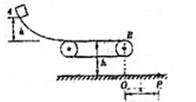
 如图所示,带弧形轨道的小车放在上表面光滑、静止浮于水面的船上,车左端被固定在船上的物体挡住,小车的弧形轨道和水平部分在B点相切,且AB段光滑,BC段粗糙.现有一个离车的BC面高为h的木块由A点自静止滑下,最终停在车面上BC段的某处.已知木块、车、船的质量分别为m1=m,m2=2m,m3=3m;木块与车表面间的动摩擦因数μ=0.4,水对船的阻力不计,求木块在BC面上滑行的距离s是多少?(设船足够长)
如图所示,带弧形轨道的小车放在上表面光滑、静止浮于水面的船上,车左端被固定在船上的物体挡住,小车的弧形轨道和水平部分在B点相切,且AB段光滑,BC段粗糙.现有一个离车的BC面高为h的木块由A点自静止滑下,最终停在车面上BC段的某处.已知木块、车、船的质量分别为m1=m,m2=2m,m3=3m;木块与车表面间的动摩擦因数μ=0.4,水对船的阻力不计,求木块在BC面上滑行的距离s是多少?(设船足够长)分析:A到B,由木块、小车、小船构成的系统机械能守恒,水平方向动量守恒,由于水的阻力不计,系统的机械能守恒,由两大守恒列式可求出木块在B点时,木块的速度和船与小车的共同速度,木块在BC间滑动时,由木块、小车组成的系统水平方向动量守恒,能量守恒,即可列式求出s.
解答:解:A到B,由木块、小车、小船构成的系统机械能守恒,水平方向动量守恒,设木块在B点时,木块的速度为v1(向右),船与小车的共同速度为v2(向左),则有:
mgh=
m
+
×5m
…①
mv1-5mv2=0…②
联立①②得:v1=
,v2=
…③
木块在BC间滑动时,由木块、小车组成的系统水平方向动量守恒,能量守恒,设系统最终的共同速度为v3,以v1的方向为正方向.
mv1-2mv2=3mv3…④
m
+
×2m
-
×3m
=μmgs…⑤
联立③④得:s=2h
答:木块在BC面上滑行的距离是2h.
mgh=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
mv1-5mv2=0…②
联立①②得:v1=
|
|
木块在BC间滑动时,由木块、小车组成的系统水平方向动量守恒,能量守恒,设系统最终的共同速度为v3,以v1的方向为正方向.
mv1-2mv2=3mv3…④
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 3 |
联立③④得:s=2h
答:木块在BC面上滑行的距离是2h.
点评:本题涉及的物体较多,关键首先要研究对象,其次要把握系统水平方向动量守恒和能量守恒两在规律,就可以列式求解了.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目