题目内容
如图所示,半径为R的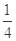 固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高
固定光滑圆轨道竖直放置,其底端与光滑的水平轨道相切于D点,O点为其圆心。质量为M的小球B静止在光滑水平轨道上,其左侧连接了一轻质弹簧;质量为m的小球A从距水平轨道高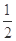 R处由静止释放,重力加速度为g,试求: ①在小球A压缩轻质弹簧到弹簧压缩到最短的过程中,弹簧对小球B的冲量大小; ②要使弹簧能再次被压缩,m与M应满足什么关系?
R处由静止释放,重力加速度为g,试求: ①在小球A压缩轻质弹簧到弹簧压缩到最短的过程中,弹簧对小球B的冲量大小; ②要使弹簧能再次被压缩,m与M应满足什么关系?
① ;②
;②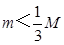
解析试题分析:(1)设A球到达圆弧底端时的速度为v0,根据机械能守恒定律有: ①,
①,
当A、B两球速度相同时,弹簧的弹性势能最大,设共同速度为v,
由动量守恒定律得:mv0=(m+M)v ②,
对小球B,由动量定理得:I=Mv,
解得: ;
;
(2)设A、B碰撞后的速度分别为v1和v2,以A的初速度方向为正方向,由动量守恒定律得:mv0=mv1+Mv2 ,由机械能守恒定律得: ,
,
解得: ,
, ,
,
要使A、B两球能发生二次碰撞,必须满足|v1|>v2 ,
则有: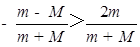 ,解得:
,解得: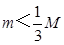 ;
;
考点:动量守恒定律及能量守恒定律。

练习册系列答案
相关题目
如图所示,一小车停在光滑水平面上,车上一人持枪向车的竖直挡板连续平射,所有子弹全部嵌在挡板内没有穿出,当射击持续了一会儿后停止,则小车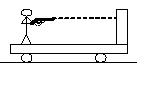
| A.速度为零 |
| B.对原静止位置的位移不为零 |
| C.将向射击方向作匀速运动 |
| D.将向射击相反方向作匀速运动 |
质量为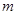 的物块甲以
的物块甲以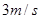 的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为
的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为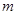 的物体乙以
的物体乙以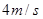 的速度与甲相向运动,如图所示。则
的速度与甲相向运动,如图所示。则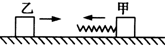
| A.甲、乙两物块在弹簧压缩过程中,由于弹力作用,动量不守恒 |
| B.当两物块相距最近时,物块甲的速率为零 |
| C.当物块甲的速率为1m/s时,物块乙的速率可能为2m/s,也可能为零 |
| D.物块甲的速率可能达到5m/s |
 、
、 ,均带正电荷,电荷量分别为
,均带正电荷,电荷量分别为 、
、 ,A、B两个小球由静止释放,重力加速度为g,则小球A和B组成的系统动量守恒应满足的关系式为 .
,A、B两个小球由静止释放,重力加速度为g,则小球A和B组成的系统动量守恒应满足的关系式为 . 初速度射入一个装有砂子的总质量为M的静止的砂车中并与车相对静止,砂车与水平地面间的摩擦可以忽略.求:
初速度射入一个装有砂子的总质量为M的静止的砂车中并与车相对静止,砂车与水平地面间的摩擦可以忽略.求: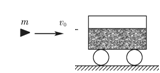
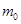 的砂子时砂车的速度
的砂子时砂车的速度 衰变,生成一
衰变,生成一 )轰击轻金属铍(
)轰击轻金属铍( )时,发现有一种贯穿能力很强的中性射线.查德威克对该粒子进行研究,进而发现了新的粒子——中子.
)时,发现有一种贯穿能力很强的中性射线.查德威克对该粒子进行研究,进而发现了新的粒子——中子.

