题目内容
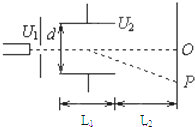
一电子(电量为e,质量为m,不计重力)从静止开始经加速电压U1加速后,以水平速度射入水平放置的两平行金属板中间,如图所示,金属板长为L1,两板距离为d,竖直放置的荧光屏距金属板右端为L2.若在两金属板间加直流电压U2时,光点偏离中线与荧光屏交点O,打在荧光屏上的P点,求:
(1)电子从加速电场出来的速度
(2)电子从偏转电场出来的动能
(3)电子在荧光屏上偏转的距离
.
(1)电子从加速电场出来的速度
(2)电子从偏转电场出来的动能
(3)电子在荧光屏上偏转的距离
| . |
| OP |

(1)粒子在加速电场中只有电场力做功,根据动能定理有:
eU1=
m
得电子加速后的速度大小为:v0=
(2)电子在偏转电场中做类平抛运动,离开电场时竖直方向的分速度为:vy=at=
?
从偏转电场出来的速度大小为:v=
则电子从偏转电场出来的动能为:
Ek=
mv2=eU1+
(3)电子在偏转电场中偏转距离为:y=
at2=
?
(
)2
偏转角度的正切为:tanθ=
=
电子离开电场后偏转距离为:y′=L2?tanθ
则有:
=y+y′=
答:(1)电子从加速电场出来的速度为
.
(2)电子从偏转电场出来的动能为eU1+
.
(3)电子在荧光屏上偏转的距离为
.
eU1=
| 1 |
| 2 |
| v | 20 |
得电子加速后的速度大小为:v0=
|
(2)电子在偏转电场中做类平抛运动,离开电场时竖直方向的分速度为:vy=at=
| eU2 |
| md |
| L1 |
| v0 |
从偏转电场出来的速度大小为:v=
|
则电子从偏转电场出来的动能为:
Ek=
| 1 |
| 2 |
e
| ||||
| 4U1d2 |
(3)电子在偏转电场中偏转距离为:y=
| 1 |
| 2 |
| 1 |
| 2 |
| eU2 |
| md |
| L1 |
| v0 |
偏转角度的正切为:tanθ=
| vy |
| v0 |
| eU2L1 | ||
md
|
电子离开电场后偏转距离为:y′=L2?tanθ
则有:
| . |
| OP |
| (L1+2L2)U2L1 |
| 4U1d |
答:(1)电子从加速电场出来的速度为
|
(2)电子从偏转电场出来的动能为eU1+
e
| ||||
| 4U1d2 |
(3)电子在荧光屏上偏转的距离为
| (L1+2L2)U2L1 |
| 4U1d |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
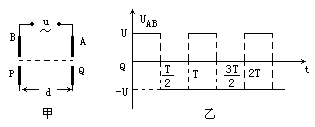
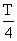 时间内放出的带电粒子才能从小孔Q中射出,则上述物理量之间应满足怎样的关系?
时间内放出的带电粒子才能从小孔Q中射出,则上述物理量之间应满足怎样的关系?