题目内容
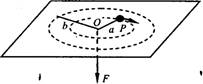
穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连，手拉细线的另一端，让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动。所有摩擦均不考虑。求：
（1）这时细线上的张力多大？
（2）若突然松开手中的细线，经时间Δt再握紧细线，随后小球沿半径为b的圆周做匀速圆周运动。试问：Δt等于多大？这时的角速度ω2为多大？
（1）这时细线上的张力多大？
（2）若突然松开手中的细线，经时间Δt再握紧细线，随后小球沿半径为b的圆周做匀速圆周运动。试问：Δt等于多大？这时的角速度ω2为多大？
解：（1）由牛顿第二定律：T=mω12a
（2）松手后小球由半径为a圆周运动到半径为b的圆周上，做的是匀速直线运动，如图所示：
（2）松手后小球由半径为a圆周运动到半径为b的圆周上，做的是匀速直线运动，如图所示：
小球匀速直线运动速度要在瞬间变到沿圆周切向，实际的运动可看做沿绳和垂直绳的两个运动同时进行
有v2＝vsinθ＝va/b
即
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
