题目内容
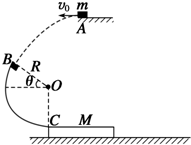
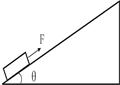
(18分)如图甲所示,在PQ左侧空间有方向斜向右上的匀强电场E1在PQ右侧空间 有一竖直向上的匀强电场E2="0.4N/C,还有垂直纸面向里的匀强磁场B(图甲中未画" 出)和水平向右的匀强电场E3 (图甲中未画出),B和E3随时间变化的情况如图乙所 示,MN为距PQ边界2.295m的竖直墙壁,现有一带正电的微粒质量为4x1O 7kg电量为1xlO 5C,从左侧电场中距PQ边界 m的A处无初速释放后,沿直线以1m/s速度垂直PQ边界进入右侧场区,设进入右侧场时刻t=0,取g = lOm/s2.求:
m的A处无初速释放后,沿直线以1m/s速度垂直PQ边界进入右侧场区,设进入右侧场时刻t=0,取g = lOm/s2.求: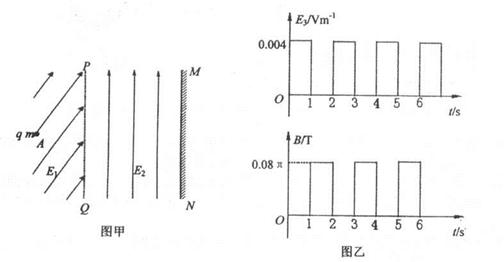
(1)PQ左侧匀强电场的电场强度E1,的大小及方向。(sin37°=0.6);
(2)带电微粒在PQ右侧场区中运动了1.5s时的速度的大小及方向;
(3)带电微粒在PQ右侧场区中运动多长时间与墙壁碰撞?( )
)
(1)E=0.5N/C,方向与水平方向成53º斜向上;(2) 1.1m/s, 方向水平向左;(3)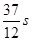
解析试题分析: (1)设PQ左侧匀强电场场强为E1,方向与水平方向夹角为θ.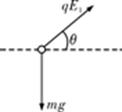
沿水平方向有 qE1cosθ=ma 1分
沿竖直方向有 qE1sinθ=mg 1分
对水平方向的匀加速运动有 v2=2as 1分
代入数据可解得 E1=0.5N/C 1分
θ=53º 1分
即E1大小为0.5N/C,方向与水平向右方向夹53º角斜向上.
(2)带电微粒在PQ右侧场区始终满足 qE2=mg 1分
在0~1s时间内,带电微粒在E3电场中 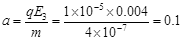 m/s2 1分
m/s2 1分
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s 1分
在1~1.5s时间内,带电微粒在磁场B中运动,周期为 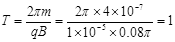 s 1分
s 1分
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在PQ右侧场区中运动了1.5s时的速度大小为1.1m/s, 方向水平向左 1分
(3)在0s~1s时间内带电微粒前进距离 s1= vt+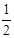 at2=1×1+
at2=1×1+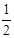 ×0.1×12=1.05m 1分
×0.1×12=1.05m 1分
带电微粒在磁场B中作圆周运动的半径
 m 1分
m 1分
因为r+s1<2.295m,所以在1s~2s时间内带电微粒未碰及墙壁.
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2
在3s内带电微粒共前进距离s3= m 1分
m 1分
在3s时带电微粒的速度大小为 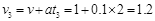 m/s 1分
m/s 1分
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径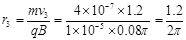 m=0.19m 1分
m=0.19m 1分
因为r3+s3>2.295m,所以在4s时间内带电微粒碰及墙壁.
带电微粒在3s以后运动情况如图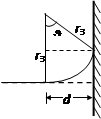

其中 d="2.295" 2.2=0.095m
sinθ=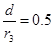
θ=30º 1分
所以,带电微粒作圆周运动的时间为 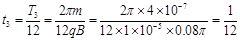 s 1分
s 1分
带电微粒与墙壁碰撞的时间为 t总=3+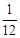 =
=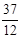 s 1分
s 1分
考点:本题关键分析清楚粒子的运动规律,然后分阶段运用牛顿第二定律、向心力公式和运动学公式列式求解.

 阅读快车系列答案
阅读快车系列答案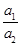 的值;
的值;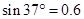 。试求:
。试求: