题目内容
如图所示，斜面体置于粗糙的水平地面上，一个质量m=2kg的物块，以υ0=10m/s的初速度沿斜面向上滑动．沿斜面向上运动过程中，经过中点时速度υ=8m/s，斜面始终静止．已知斜面的倾角θ=37°，长l=4.5m．空气阻力不计，取sin37°=0.6，cos37°=0.8，g=10m/s2．求：
（1）物块从底端运动到中点的时间；
（2）试分析物块从开始运动到落地前所经历的运动形式，并说明其加速度的大小和方向；
（3）物块在斜面上运动时，斜面体受到水平地面摩擦力的大小和方向．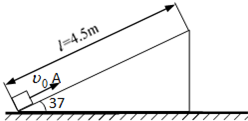
（1）物块从底端运动到中点的时间；
（2）试分析物块从开始运动到落地前所经历的运动形式，并说明其加速度的大小和方向；
（3）物块在斜面上运动时，斜面体受到水平地面摩擦力的大小和方向．
（1）物块在斜面上做匀减速运动：
=
=9m/s，t=
=0.25s
（2）物块运动斜面顶端的速度为υt
从底端到顶端：υt2-υ02=2aX
即：υt 2-102=2a×4.5
从底端到中点：υ中2-υ02=2aS
即：82-102=2a×2.25
解得a=-8m/s2 υt=
m/s
物块运动分为两个阶段：一是沿斜面向上的匀减速运动，加速度大小为8m/s2，方向沿斜面向下；二是抛体运动，加速度大小为重力加速度g=10m/s2，方向竖直向下．
（3）先求滑动摩擦因数 物块沿斜面做匀减速运动：mgsinθ+μmgcosθ=maμ=0.25
对斜面体受力分析（如图所示）并建立坐标系，在X方向上：
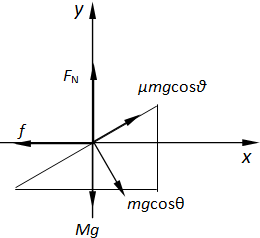
f=（μmgcosθ）cosθ+（mgcosθ）sinθ=12.8N
故答案为：（1）物块从底端运动到中点的时间t=0.25s
（2）物块运动分为两个阶段：一是沿斜面向上的匀减速运动，加速度大小为8m/s2，方向沿斜面向下；二是抛体运动，加速度大小为重力加速度g=10m/s2，方向竖直向下
（3）物块在斜面上运动时，斜面体受到水平地面摩擦力的大小为12.8N和方向沿水平向左．
| . |
| V |
| υ0+υ中 |
| 2 |
| S | ||
|
（2）物块运动斜面顶端的速度为υt
从底端到顶端：υt2-υ02=2aX
即：υt 2-102=2a×4.5
从底端到中点：υ中2-υ02=2aS
即：82-102=2a×2.25
解得a=-8m/s2 υt=
| 28 |
物块运动分为两个阶段：一是沿斜面向上的匀减速运动，加速度大小为8m/s2，方向沿斜面向下；二是抛体运动，加速度大小为重力加速度g=10m/s2，方向竖直向下．
（3）先求滑动摩擦因数 物块沿斜面做匀减速运动：mgsinθ+μmgcosθ=maμ=0.25
对斜面体受力分析（如图所示）并建立坐标系，在X方向上：
f=（μmgcosθ）cosθ+（mgcosθ）sinθ=12.8N
故答案为：（1）物块从底端运动到中点的时间t=0.25s
（2）物块运动分为两个阶段：一是沿斜面向上的匀减速运动，加速度大小为8m/s2，方向沿斜面向下；二是抛体运动，加速度大小为重力加速度g=10m/s2，方向竖直向下
（3）物块在斜面上运动时，斜面体受到水平地面摩擦力的大小为12.8N和方向沿水平向左．
练习册系列答案
智能训练练测考系列答案
相关题目
如图所示，斜面体置于光滑水平地面上，其光滑斜面上有一物体由静止沿斜面下滑，在物体下滑过程中，下列说法正确的是（ ）
（2013?潍坊二模）如图所示，斜面体置于粗糙水平面上，斜面光滑．小球被轻质细线系住放在斜面上．细线另一端跨过定滑轮，用力拉细线使小球沿斜面缓慢移动一段距离，斜面体始终静止．移动过程中（ ）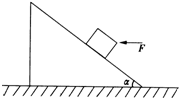
如图所示，斜面体置于水平地面上，物体在水平力F的作用下静止在斜面上，若稍许增大水平力，而使物体仍能保持静止．则（ ）
如图所示，斜面体置于粗糙的水平地面上，一个质量m=2kg的物块，以υ0=10m/s的初速度沿斜面向上滑动．沿斜面向上运动过程中，经过中点时速度υ=8m/s，斜面始终静止．已知斜面的倾角θ=37°，长l=4.5m．空气阻力不计，取sin37°=0.6，cos37°=0.8，g=10m/s2．求：