Question

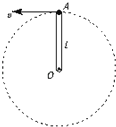
【题目】如图所示，用长为L的细绳把质量为m的小球系于O点，把细绳拉直至水平后无初速度地释放，小球运动至O点正下方的B点时绳子恰好被拉断，B点距地面的高度也为L．设绳子被拉断时小球没有机械能损失，小球抛出后落到水平地面上的C点求: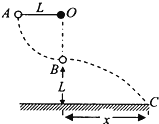

（1）绳子被拉断前瞬间受到的拉力大小T．
（2）B、C两点间的水平距离x．

Answer 1

【答案】
（1）

设小球在B点的速度为v，由A到B有：mgh= mv2　

解得：v= ．

设绳子被拉断瞬间受到的拉力大小为T，由牛顿运动定律有：T﹣mg=m ，

将v= 代入得：T=3mg

（2）

绳子被拉断后，小球做平抛运动，有：L= gt2　

x=vt　　

将v= 代入得：x=2L

【解析】（1）设小球在B点的速度为v，由A到B有：mgh= mv2
解得：v= ．
设绳子被拉断瞬间受到的拉力大小为T，由牛顿运动定律有：T﹣mg=m ，
将v= 代入得：T=3mg（2）绳子被拉断后，小球做平抛运动，有：L= gt2
x=vt
将v= 代入得：x=2L
答：（1）绳子被拉断前瞬间受到的拉力大小T为3mg ． （2）B、C两点间的水平距离x为2L ．
【考点精析】通过灵活运用向心力，掌握向心力总是指向圆心，产生向心加速度，向心力只改变线速度的方向，不改变速度的大小；向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时，千万不可在物体受力之外再添加一个向心力即可以解答此题．