题目内容
13.把地球看成半径为R的均匀球体,已知地球表面的重力加速度为g,自转周期为T,不考虑地球自转对物体重力的影响,求:(1)地球的第一宇宙速度;
(2)地球同步卫星离地面的高度.
分析 (1)第一宇宙速度是卫星在近地圆轨道上的环绕速度,重力等于万有引力,引力等于向心力,列式求解;
地球的同步卫星的万有引力提供向心力,可以求出地球同步卫星的高度
解答 解:(1)第一宇宙速度等于近地卫星的环绕速度,
对近地卫星列牛顿第二定律方程有
$mg=m\frac{{{v}_{1}}^{2}}{R}$
解得第一宇宙速度 ${v}_{1}=\sqrt{gR}$
(2)对地球的同步卫星的万有引力提供向心力,列牛顿第二定律方程
有 $\frac{GMm}{(R+h)^{2}}=m\frac{4{π}^{2}(R+h)}{{T}^{2}}$
式中 GM=gR2
联立解得 h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R
答:(1)地球第一宇宙速度是$\sqrt{gR}$;
(2)地球同步卫星距离地面的高度是为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R.
点评 解答此题要清楚地球表面的物体受到的重力等于万有引力,地球的同步卫星的万有引力提供向心力.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4. 如图甲所示的电路中,理想变压器原、副线圈匝数之比为5:1,原线圈接入图乙所示的电压,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻(其阻值随温度的升高而减小),下列说法中正确的是( )
如图甲所示的电路中,理想变压器原、副线圈匝数之比为5:1,原线圈接入图乙所示的电压,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻(其阻值随温度的升高而减小),下列说法中正确的是( )
 如图甲所示的电路中,理想变压器原、副线圈匝数之比为5:1,原线圈接入图乙所示的电压,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻(其阻值随温度的升高而减小),下列说法中正确的是( )
如图甲所示的电路中,理想变压器原、副线圈匝数之比为5:1,原线圈接入图乙所示的电压,副线圈接火灾报警系统(报警器未画出),电压表和电流表均为理想电表,R0为定值电阻,R为半导体热敏电阻(其阻值随温度的升高而减小),下列说法中正确的是( )| A. | 图乙中电压的有效值为110V | |
| B. | 电压表的示数为44V | |
| C. | R处出现火警时,电流表示数增大 | |
| D. | R处出现火警时,电阻R0消耗的电功率减小 |
1.真空中有一对平行金属板,相距2.8cm,两板电势能差为32V,二价的氧离子由静止开始加速,从一个极板到另一个极板时,动能是( )
| A. | 2.8eV | B. | 5.6eV | C. | 32eV | D. | 64eV |
8.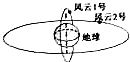 我国气象卫星有两类:一类是极地轨道卫星,如图中所示的风云1号,绕地球做匀速圆周运动的周期为12h,另一类是地球同步轨道卫星,如图2所示的风云2号,绕地球做匀速圆周运动的周期为24h.下列说法正确的是( )
我国气象卫星有两类:一类是极地轨道卫星,如图中所示的风云1号,绕地球做匀速圆周运动的周期为12h,另一类是地球同步轨道卫星,如图2所示的风云2号,绕地球做匀速圆周运动的周期为24h.下列说法正确的是( )
 我国气象卫星有两类:一类是极地轨道卫星,如图中所示的风云1号,绕地球做匀速圆周运动的周期为12h,另一类是地球同步轨道卫星,如图2所示的风云2号,绕地球做匀速圆周运动的周期为24h.下列说法正确的是( )
我国气象卫星有两类:一类是极地轨道卫星,如图中所示的风云1号,绕地球做匀速圆周运动的周期为12h,另一类是地球同步轨道卫星,如图2所示的风云2号,绕地球做匀速圆周运动的周期为24h.下列说法正确的是( )| A. | 风云1号、风云2号相对地面均静止 | |
| B. | 风云1号的线速度大于风云2号的线速度 | |
| C. | 风云1号的角速度小于风云2号的角速度 | |
| D. | 风云1号的向心加速度大于风云2号的向心加速度 |
5. 光导纤维被认为是20世纪最伟大的发明之一,2009年诺贝尔物理学奖授予被誉为“光纤之父”的华裔科学家高锟,以下关于光导纤维的说法中正确的是( )
光导纤维被认为是20世纪最伟大的发明之一,2009年诺贝尔物理学奖授予被誉为“光纤之父”的华裔科学家高锟,以下关于光导纤维的说法中正确的是( )
 光导纤维被认为是20世纪最伟大的发明之一,2009年诺贝尔物理学奖授予被誉为“光纤之父”的华裔科学家高锟,以下关于光导纤维的说法中正确的是( )
光导纤维被认为是20世纪最伟大的发明之一,2009年诺贝尔物理学奖授予被誉为“光纤之父”的华裔科学家高锟,以下关于光导纤维的说法中正确的是( )| A. | 内芯的折射率比外套的小,光传播时在外套与空气的界面上发生全反射 | |
| B. | 内芯的折射率比外套的小,光传播时在内芯与外套的界面上发生全反射 | |
| C. | 内芯的折射率比外套的大,光传播时在外套与空气的界面上发生全反射 | |
| D. | 内芯的折射率比外套的大,光传播时在内芯与外套的界面上发生全反射 |
12.电磁炮有很多优点,备受各国军事家的重视,如图是导轨式电磁炮实验装置的示意图.两根平行长直金属导轨沿水平方向固定,其间安放金属滑块(即实验用弹丸).滑块可沿导轨无摩擦滑行,且始终与导轨保持良好接触.电源提供的强大电流从一根导轨流入,经过滑块,再从另一导轨流回电源.滑块被导轨中的电流形成的磁场推动而发射.在发射过程中,滑块所在位置始终可以简化为匀强磁场,方向垂直于纸面,其强度与电流的关系为B=kI,.如果两导轨内侧间距为l,滑块的质量为m,滑块沿导轨滑行距离s后获得的发射速度为v0.以下说法中正确的是( )


| A. | 若使电流和磁感应强度的方向同时反向,滑块的发射方向也将随之反向 | |
| B. | 若将电源提供的电流加倍,则滑块沿导轨滑行距离s后获得的发射速度为2v | |
| C. | 若使电源提供的电流加倍,则滑块沿导轨滑行距离s后获得的发射速度为4v | |
| D. | 若使滑块的质量加倍,则滑块沿导轨滑行距离s后获得的发射速度为0.5v |
10.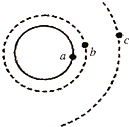 如图所示,a为地球赤道上的待发射卫星,b为赤道上空近地圆轨道卫星,c为地球同步卫星.三颗卫星质量相同.三颗卫星的线速度分别为va、vb、vc,角速度分别为ωa、ωb、ωc,周期分别为Ta、Tb、Tc,向心力分别为Fa、Fb、Fc,则( )
如图所示,a为地球赤道上的待发射卫星,b为赤道上空近地圆轨道卫星,c为地球同步卫星.三颗卫星质量相同.三颗卫星的线速度分别为va、vb、vc,角速度分别为ωa、ωb、ωc,周期分别为Ta、Tb、Tc,向心力分别为Fa、Fb、Fc,则( )
 如图所示,a为地球赤道上的待发射卫星,b为赤道上空近地圆轨道卫星,c为地球同步卫星.三颗卫星质量相同.三颗卫星的线速度分别为va、vb、vc,角速度分别为ωa、ωb、ωc,周期分别为Ta、Tb、Tc,向心力分别为Fa、Fb、Fc,则( )
如图所示,a为地球赤道上的待发射卫星,b为赤道上空近地圆轨道卫星,c为地球同步卫星.三颗卫星质量相同.三颗卫星的线速度分别为va、vb、vc,角速度分别为ωa、ωb、ωc,周期分别为Ta、Tb、Tc,向心力分别为Fa、Fb、Fc,则( )| A. | ωa=ωb=ωc | B. | Ta=Tc>Tb | C. | va=vb<vc | D. | Fa=Fb<Fc |
 某物理兴趣小组在探究平抛运动的规律实验时,分成两组,其中一个实验小组让小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到如图所示的照片,已知每个小方格边长0.1m,当地的重力加速度为g=10m/s2.其中C点处的位置坐标已被污迹覆盖.
某物理兴趣小组在探究平抛运动的规律实验时,分成两组,其中一个实验小组让小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到如图所示的照片,已知每个小方格边长0.1m,当地的重力加速度为g=10m/s2.其中C点处的位置坐标已被污迹覆盖.