题目内容

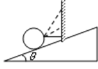
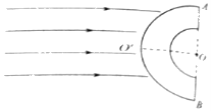
【题目】如图所示，均匀透明介质制成的半圆筒，O为圆心、AB为直径，OO′垂直于AB，外圆半径为a、内圆半径为a，一束与OO′平行的光射向圆筒。进入透明介质折射角为30°的入射光线恰好不能射入圆筒内部。求：

（1）均匀介质的折射率

（2）若在光线入射方向垂直放置一块不透光的遮光板，使圆筒内部没有任何光线，遮光板的最小宽度？

【答案】（1）均匀介质的折射率是;（2）若在光线入射方向垂直放置一块不透光的遮光板，使圆筒内部没有任何光线，遮光板的最小宽度为2a。

【解析】

（1）在三角形ODC中，由正弦定理得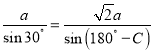

解得 sinC＝

则均匀介质的折射率

（2）光进入圆筒时，由折射定律得

解得 i＝45°

DF＝asin45°＝a

所以遮光板的最小宽度为2a

练习册系列答案
相关题目

【题目】如图所示为远距离交流输电的简化电路图。发电厂的输出电压是U，用等效总电阻是r的两条输电线输电，输电线路中的电流是I1，其末端间的电压为U1。在输电线与用户间连有一理想变压器，流入用户端的电流是I2。则（ ）

A. 用户端的电压为I1U1/I2

B. 输电线上的电压降为U

C. 理想变压器的输入功率为I12r

D. 输电线路上损失的电功率为I1U

【题目】如图1所示是在做“验证牛顿第二定律”的实验时的装置，实验中使用的是电火花打点计时器，所用的电源是________（填“直流”或“交流”）电源，电压为________V，频率是50Hz．放在水平桌面的小车（包括里面的钩码）的总质量为M，悬挂的每个钩码的质量为m．挂一个钩码时，水平木板上的小车恰好匀速运动，挂5个同样钩码时小车带动的纸带如图2所示，每相邻两点之间有四个点没有画出来，纸带上数字的单位是厘米，都是该点到点“0”的距离，该纸带________（填“是”或“不是”）从开始的“0”点就做匀加速直线运动．小车做匀加速直线运动段的加速度a=________m/s2（保留三位有效数字），g=9.8m/s2，=________（用分数表示）．

【题目】对电容C＝，以下说法正确的是

A.电容器带电荷量越大，电容就越大

B.对于固定电容器，它的带电荷量跟它两极板间所加电压的比值保持不变

C.可变电容器的带电荷量跟加在两极板间的电压成反比

D.如果一个电容器没有电压，就没有带电荷量，也就没有电容

【题目】（1）在测量电阻丝电阻率的实验中，用刻度尺测量被测电阻丝的有效长度，如图所示，金属丝的另一端与刻度尺的零刻度对齐，读数为____cm。用螺旋测微器测金属丝直径，结果如图所示，读数为____mm。

（2）电压表、电流表读数如图，则U=___ A，I= ___V。

（3）根据电路图给实物图连线（_____）

【题目】如图所示，小球用细绳系住，放在倾角为的固定光滑斜面上。当细绳由水平方向逐渐向上偏移的过程中小球始终静止在斜面上，绳对球的拉力F和斜面对小球的支持力将

A.F逐渐增大，逐渐减小B.F先增大后减小，逐渐减小

C.F逐渐增大，逐渐增大D.F先减小后增大，逐渐减小

【题目】如图，图象反映了甲、乙两车在同一条直道上行驶的位置随时间变化的关系，已知乙车做匀变速直线运动，其图线与t轴相切于10s处，下列说法正确的是

A. 5s时两车速度相等 B. 甲车的速度为

C. 乙车的加速度大小为 D. 乙车的初位置在处

【题目】某同学乘坐动车时，观察到车厢内电子屏上显示如图所示，则

A.9:03指的是时刻，180km/h是瞬时速度

B.9:03指的是时刻，180km/h是平均速度

C.9:03指的是时间，180km/h是平均速度

D.9:03指的是时间，180km/h是瞬时速度

【题目】一辆值勤的警车停在平直公路边，当警员发现从他旁边以v=8 m/s的速度匀速驶过的货车有违章行为时，决定前去追赶，经2.5 s，警车发动起来，以加速度a=2 m/s2做匀加速运动，试问：

（1）警车发动起来后要多长时间才能追上违章的货车？

（2）在警车追上货车之前，两车间的最大距离是多少？

（3）若警车的最大速度是12 m/s，则警车发动起来后要多长时间才能追上违章的货车？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网