题目内容
8.地球同步卫星的质量为m.距地面高度为h,地球半径为R,地面处重力加速度为g,地球自转角速度为ω,则若以m、h、R、g来表示地球对卫星的引力大小为$\frac{mg{R}^{2}}{(R+h)^{2}}$.分析 由题知地球的同步卫星的轨道半径为R+h.根据地球的半径和地球表面的重力加速度,由重力等于万有引力,可求出地球的质量.地球的同步卫星的角速度与地球的自转的角速度相同,轨道平面必须与赤道平面重合.由向心力公式求解向心力
解答 解:该卫星所受地球的万有引力为:F=$\frac{GMm}{(R+h)^{2}}$,
由mg=$\frac{GMm}{{R}^{2}}$得到GM=gR2,
联立解得:F=$\frac{mg{R}^{2}}{(R+h)^{2}}$,
故答案:$\frac{mg{R}^{2}}{(R+h)^{2}}$
点评 该题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,解题过程中注意黄金代换式的应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线,下列说法中正确的是( )
如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线,下列说法中正确的是( )
 如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线,下列说法中正确的是( )
如图所示,在匀速转动的水平圆盘上,沿半径方向放着用细线相连的质量相等的两个物体A和B,它们与盘间的摩擦因数相同,当圆盘转动到两个物体刚好还未发生滑动时,烧断细线,下列说法中正确的是( )| A. | 两个物体刚好还未发生滑动时,两物体所受的摩擦力均为最大静摩擦力 | |
| B. | 烧断细线,两物体沿切向方向滑动 | |
| C. | 烧断细线,物体B仍随圆盘一起做匀速圆周运动,物体A发生滑动,离圆盘圆心越来越远 | |
| D. | 烧断细线,两物体仍随圆盘一起做圆周运动,不发生滑动 |
16.当线圈在匀强磁场中绕垂直于磁场方向的轴旋转时,线圈中所产生的最大感应电动势的大小与下列哪些因素无关?( )
| A. | 线圈平面的形状 | B. | 线圈的匝数 | ||
| C. | 线圈的面积 | D. | 线圈转动的角速度 |
20. 如图所示,质量为m的小球用长L的细线悬挂而静止在A点.用水平拉力F将小球缓慢地从A点拉到B点,直至细线成水平状态,该过程中拉力F做功为( )
如图所示,质量为m的小球用长L的细线悬挂而静止在A点.用水平拉力F将小球缓慢地从A点拉到B点,直至细线成水平状态,该过程中拉力F做功为( )
 如图所示,质量为m的小球用长L的细线悬挂而静止在A点.用水平拉力F将小球缓慢地从A点拉到B点,直至细线成水平状态,该过程中拉力F做功为( )
如图所示,质量为m的小球用长L的细线悬挂而静止在A点.用水平拉力F将小球缓慢地从A点拉到B点,直至细线成水平状态,该过程中拉力F做功为( )| A. | FL | B. | $\frac{πFL}{2}$ | C. | mgL | D. | 0 |
17.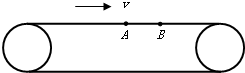 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.则下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.则下列说法正确的是( )
 如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.则下列说法正确的是( )
如图所示,传送带以恒定速率v运动,现将质量都是m的小物体甲、乙(视为质点)先后轻轻放在传送带的最左端,甲到达A处时恰好达到速率v,乙到达B处时恰好达到速率v.则下列说法正确的是( )| A. | 甲、乙两物块在传送带上加速运动时具有的加速度相同 | |
| B. | 甲、乙两物块在传送带上加速运动时间相等 | |
| C. | 传送带对甲、乙两物体做功相等 | |
| D. | 传送带对甲、乙两物体做功不相等 |
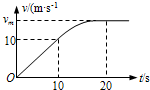 某模型汽车的质量为2kg,在水平面上做测试时,先以恒定牵引力F=12N从静止开始做匀加速运动,10s末速度达到10m/s时,发动机功率恰好达到最大值.从该时刻起,汽车保持该最大功率继续加速,经历一段时间后,汽车达到了最大速度.上述过程模型汽车的v-t图象如图所示.由以上信息可知:模型汽车牵引力的最大功率Pm=120W;模型汽车做匀加速运动阶段的加速度大小为a=1m/s2;本次测试的前20s内汽车牵引力做的功为W=1800J.
某模型汽车的质量为2kg,在水平面上做测试时,先以恒定牵引力F=12N从静止开始做匀加速运动,10s末速度达到10m/s时,发动机功率恰好达到最大值.从该时刻起,汽车保持该最大功率继续加速,经历一段时间后,汽车达到了最大速度.上述过程模型汽车的v-t图象如图所示.由以上信息可知:模型汽车牵引力的最大功率Pm=120W;模型汽车做匀加速运动阶段的加速度大小为a=1m/s2;本次测试的前20s内汽车牵引力做的功为W=1800J.
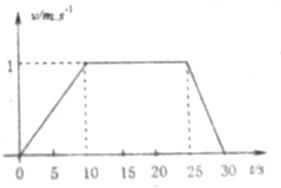 一质量为m=40kg的小孩站在电梯水平地板上,电梯从t=0时刻由静止开始竖直上升,速度随时间变化规律如图所示,取g=10m/s2,求:
一质量为m=40kg的小孩站在电梯水平地板上,电梯从t=0时刻由静止开始竖直上升,速度随时间变化规律如图所示,取g=10m/s2,求: