��Ŀ����
19�� ��ͼ��ʾΪһ���ʾ���ܣ����Ӵӵ�˿K���������ٶȲ��ƣ�������˿��A���ļ��ٵ�ѹU1���٣���A�����Ŀ���������KO�����Ȼ���������ƽ�н�����M��N�γɵ�ƫת�糡�У�ƫת�糡����Ϊ��ǿ�糡�������ӽ���M��N��糡ʱ���ٶ���糡����ֱ�����Ӿ���ƫת�糡�����ӫ�����ϵ�P�㣮��֪���ٵ�ѹΪU1��M��N�����ĵ�ѹΪU2�������ľ���Ϊd���峤ΪL1�����Ҷ˵�ӫ�����ľ���ΪL2�����ӵ�����Ϊm�������Ϊe����
��ͼ��ʾΪһ���ʾ���ܣ����Ӵӵ�˿K���������ٶȲ��ƣ�������˿��A���ļ��ٵ�ѹU1���٣���A�����Ŀ���������KO�����Ȼ���������ƽ�н�����M��N�γɵ�ƫת�糡�У�ƫת�糡����Ϊ��ǿ�糡�������ӽ���M��N��糡ʱ���ٶ���糡����ֱ�����Ӿ���ƫת�糡�����ӫ�����ϵ�P�㣮��֪���ٵ�ѹΪU1��M��N�����ĵ�ѹΪU2�������ľ���Ϊd���峤ΪL1�����Ҷ˵�ӫ�����ľ���ΪL2�����ӵ�����Ϊm�������Ϊe������1�����Ӵ���A��ʱ���ٶ�v0��С��
��2�����Ӵ�ƫת�糡���ʱ�ص糡����IJ�����y1��
��3�����Ӵ���ӫ������P��ʱ�Ķ���EK���ٶȷ�����������KO�нǵ�����ֵtan�ȣ�
��4�����Ӿ���ƫת�糡�����ӫ������P�㵽ӫ��������O��ľ���Y�Լ�����ʱ��t2��
���� ��1����ֱ���ٹ��̸��ݶ��ܶ�����ʽ��⣻
��2���������ٶ�v0����ƫת�糡��������ƽ���˶�����������ƽ���˶��ķ��˶���ʽ��ʽ��⼴�ɣ�
��3���Ե��Ӵӽ���ƫת�糡������ӫ����P����̸��ݶ��ܶ�����ʽ���ĩ���ܣ����ݷ��ٶȹ�ʽ����ٶȷ�����������KO�нǵ�����ֵtan�ȣ�
��4�������뿪ƫת�糡��������ֱ���˶���ˮƽ���˶�������ֱ���˶�������ƽ���˶���ĩ�ٶȵķ����ӳ���ͨ��ˮƽ��λ�Ƶ��е㣮
��� �⣺��1������Ӿ���ѹU1���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�
e U1=$\frac{1}{2}mv_0^2$����ã�${v_0}=\sqrt{\frac{{2e{U_1}}}{m}}$
��2���������ٶ�v0����ƫת�糡��ֱ�ڵ糡����������ֱ���˶����ص糡���������ٶ�Ϊ����ȼ���ֱ���˶�����ƫת�糡�ĵ糡ǿ��ΪE��������ƫת�糡�˶���ʱ��Ϊt1�����ӵļ��ٶ�Ϊa���뿪ƫת�糡ʱ�����ԭ�˶�����IJ�����Ϊy1������ţ�ٵڶ����ɺ��˶�ѧ��ʽ�ã�
F=eE��E=$\frac{U_2}{d}$��F=ma��a=$\frac{{e{U_2}}}{md}$
t1=$\frac{L_1}{v_0}$��y1=$\frac{1}{2}at_1^2$����ã�y1=$\frac{{{U_2}L_1^2}}{{4{U_1}d}}$
��3�������뿪ƫת�糡��������ֱ���˶��������ӽ���ƫת�糡������ӫ����P�㣬�糡�����Ĺ���
W2=Fy1=$\frac{{e{y_1}{U_2}}}{d}$=EK-$\frac{1}{2}mv_0^2$
��ã�EK=e U1+$\frac{e{U}_{2}^{2}{L}_{1}^{2}}{4{U}_{1}{{d}^{2}}_{\;}}$
������뿪ƫת�糡ʱ�ص糡�����ٶ�Ϊvy�������˶�ѧ��ʽ��vy=at1=$\frac{{e{U_2}{L_1}}}{{dm{v_0}}}$
�����Ӵ���ӫ������P��ʱ���ٶȷ�����������KO�н�������뿪ƫת�糡ƫת�Ǧ���ͬ����
tan��=$\frac{v_y}{v_x}$=$\frac{e{U}_{2}{L}_{1}}{dm{v}_{\;}^{2}}$=$\frac{{U}_{2}{L}_{1}}{2d{U}_{1}}$
��4��������뿪ƫת�糡�����ӫ���������õ�ʱ��Ϊt2�����Ӵ�ӫ�����ϵIJ�����Ϊy2����ͼ��ʾ��
t2=$\frac{L_2}{v_0}$��y2=vyt2
��ã�y2=$\frac{{{U_2}{L_1}{L_2}}}{{2d{U_1}}}$
P��O��ľ���Ϊ��
Y=y1+y2=$\frac{{��2{L_2}+{L_1}��{U_2}{L_1}}}{{4{U_1}d}}$
��Y=�� L2+$\frac{L_1}{2}$��tan��=$\frac{{��2{L_2}+{L_1}��{U_2}{L_1}}}{{4{U_1}d}}$��
t2=$\frac{L_2}{v_0}$
�𣺣�1�����Ӵ���A��ʱ���ٶ�v0��СΪ$\sqrt{\frac{2e{U}_{1}}{m}}$��
��2�����Ӵ�ƫת�糡���ʱ�ص糡����IJ�����y1Ϊ$\frac{{U}_{2}{L}_{1}^{2}}{4{U}_{1}d}$��
��3�����Ӵ���ӫ������P��ʱ�Ķ���ΪeU1+$\frac{e{U}_{2}^{2}{L}_{1}^{2}}{4{U}_{1}{{d}^{2}}_{\;}}$���ٶȷ�����������KO�нǵ�����ֵΪ$\frac{{U}_{2}{L}_{1}}{2d{U}_{1}}$��
��4�����Ӿ���ƫת�糡�����ӫ������P�㵽ӫ��������O��ľ���YΪ$\frac{��2{L}_{2}+{L}_{1}��{U}_{2}{L}_{1}}{4{U}_{1}d}$������ʱ��Ϊ$\frac{{L}_{2}}{{v}_{0}}$��
���� ���������ڵ糡����ƽ���˶����о�������ƽ���˶����ƣ������˶��ĺϳ���ֽ⣬������������������ĸ�϶࣬����дʱһ��Ҫϸ�ģ�

| A�� | �ٶȴ��ʱ�䳤 | B�� | �ٶ�С��ʱ�䳤 | ||
| C�� | �����ٶȴ�С��������ͬʱ��� | D�� | ��ص�ʱ�䳤����������������� |
| A�� | �ڸò����д���ʱ��������ٶȽϴ� | |
| B�� | ����ͬ������Ǵӿ���б����ò����У����������ǽϴ� | |
| C�� | �Ӹò����������������ȫ����ʱ������ٽ�ǽ�С | |
| D�� | ��ͬһװ�ý���˫�����ʵ�飬������������Ƽ���С |
 ���Ӹ�Ӧ���������ñ仯�Ĵų������ٵ��ӣ�������ƽ���뾶ΪR�Ļ��ι�������λ����չܵ��ڣ��˶����Ÿ�Ӧǿ�ȷ����뻷�ι��ƽ�洹ֱ�����ӱ���Ӧ�糡���٣���Ӧ�糡�ķ����뻷�ι�����У����ӵ����Ϊe��
���Ӹ�Ӧ���������ñ仯�Ĵų������ٵ��ӣ�������ƽ���뾶ΪR�Ļ��ι�������λ����չܵ��ڣ��˶����Ÿ�Ӧǿ�ȷ����뻷�ι��ƽ�洹ֱ�����ӱ���Ӧ�糡���٣���Ӧ�糡�ķ����뻷�ι�����У����ӵ����Ϊe�� ��ͼ��ʾΪһ������ֱ���˶���v-tͼ����ͼ����
��ͼ��ʾΪһ������ֱ���˶���v-tͼ����ͼ����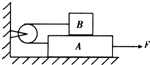 ��ͼ��ʾ��λ��ˮƽ�����ϵ����A����Ϊ2m���ɿ�������ֵ�����������Ϊm�����B�������ӻ��ֵ�A�͵�B������������ˮƽ�ģ���֪B��A֮��Ķ�Ħ�������Ǧ̣�A������֮��Ķ�Ħ��������2�̣����ֵ��������������ϵ�Ħ�������ƣ�����һˮƽ���ҵ���F��Aʹ���������˶�����F�Ĵ�СΪ��������
��ͼ��ʾ��λ��ˮƽ�����ϵ����A����Ϊ2m���ɿ�������ֵ�����������Ϊm�����B�������ӻ��ֵ�A�͵�B������������ˮƽ�ģ���֪B��A֮��Ķ�Ħ�������Ǧ̣�A������֮��Ķ�Ħ��������2�̣����ֵ��������������ϵ�Ħ�������ƣ�����һˮƽ���ҵ���F��Aʹ���������˶�����F�Ĵ�СΪ�������� ��ͼ��ʾ��ˮƽ������Ͽ���һ�ܷɻ��ڽ���Ͷ��ѵ�����ɻ���ˮƽ�������ȼ���ֱ���˶������ɻ��ɾ��۲��B�����Ϸ�A��ʱͶ��һ��ը������ʱ��Tը�����ڹ۲��B��ǰ��L1����C�㣬���ͬʱ�ɻ�Ͷ�ų��ڶ���ը�����������ھ�۲��B��ǰ��L2����D�㣬��L2=3L1�������������ƣ�
��ͼ��ʾ��ˮƽ������Ͽ���һ�ܷɻ��ڽ���Ͷ��ѵ�����ɻ���ˮƽ�������ȼ���ֱ���˶������ɻ��ɾ��۲��B�����Ϸ�A��ʱͶ��һ��ը������ʱ��Tը�����ڹ۲��B��ǰ��L1����C�㣬���ͬʱ�ɻ�Ͷ�ų��ڶ���ը�����������ھ�۲��B��ǰ��L2����D�㣬��L2=3L1�������������ƣ�