��Ŀ����
����Ŀ����ͼ��ʾ����ƽ�н��������ľ���L=0.2m�������������ڵ�ƽ����ˮƽ��нǦ�=37�㣬���������һ�˽��е綯��E=6V������r=1����ֱ����Դ���ְ�һ������![]() �ĵ����ab���ڽ��������ϣ��������������촹ֱ���ҽӴ����ã�����֮��Ķ�Ħ������Ϊ��=0.5��Ϊʹ������ܾ�ֹ�ڵ����ϣ��ڵ�������ƽ���ڣ���һ����ֱ���ϵ���ǿ�ų���������費�ƣ�����������·�ĵ���R0=2������֪sin37��=0.6��cos37��=0.8��ȡg=10m/s2����
�ĵ����ab���ڽ��������ϣ��������������촹ֱ���ҽӴ����ã�����֮��Ķ�Ħ������Ϊ��=0.5��Ϊʹ������ܾ�ֹ�ڵ����ϣ��ڵ�������ƽ���ڣ���һ����ֱ���ϵ���ǿ�ų���������費�ƣ�����������·�ĵ���R0=2������֪sin37��=0.6��cos37��=0.8��ȡg=10m/s2����
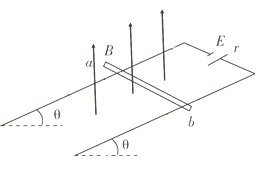
��1�����Ÿ�Ӧǿ��B1���ʱ��������뵼����Ħ����Ϊ�㣻
��2�����Ÿ�Ӧǿ��B2=12.5Tʱ��������뵼���Ħ�����Ĵ�С�ͷ���
��3��ʹ������ܾ�ֹ�ڵ��������Ӵų��ĴŸ�Ӧǿ��B����Сֵ��
���𰸡���1��6.25T ��2��![]() ��3��
��3��![]()
����������1�����ݱպϵ�·��ŷķ���ɣ�����![]()
��ƽ�������ã� ![]() ����
����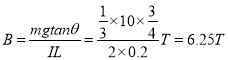
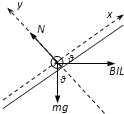
��2����������������ͼ��ʾ(ͼ��Ħ����fδ����)
���Ÿ�Ӧǿ��![]() ʱ��
ʱ�� ![]()
Ħ����f��б����������ƽ�������ã� ![]()
�������ݵã� ![]()
��3�����Ÿ�Ӧǿ��B��Сʱ�������ǡ�ò��»�����ʱĦ����f��б�����ϣ�
���� ![]()
���� ![]()
�֣� ![]()
�����ã� 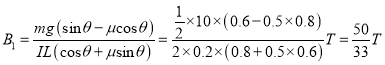

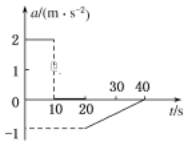
����Ŀ��һ�������Ӿ�ֹ��ʼ�ȼ���ֱ�߿�����Ȼ������ֱ���˶���������ȼ���ֱ���˶���ֱ��ֹͣ���������˲�ͬʱ���������ٶȣ����ݱ����֪��������
ʱ��/s | 1 | 2 | 3 | 5 | 6 | 7 | 9.5 | 10.5 |
�ٶ�/��ms��1�� | 3 | 6 | 9 | 12 | 12 | 12 | 9 | 3 |
A. ������t=5sʱ�̿�ʼ������ֱ���˶�
B. ���������˶���ʱ��Ϊ5s
C. �����ӿ�ʼ�˶�ֱ��ֹͣ�Ĺ����е�ƽ���ٶȴ�СԼ8.73m/s
D. �������ٶε�ƽ���ٶ�С�ڼ��ٶε�ƽ���ٶ�