题目内容
现有一种特殊的电池,它的电动势E约为9V,内阻r约为50Ω,已知该电池允许输出的最大电流为50mA.为了测定这个电池的电动势和内阻,某同学利用如图(a)所示的电路进行实验.图中电压表的内阻很大,对电路和影响可不考虑,R为电阻箱,阻值范围0~9999Ω,R.是定值电阻,起保护电路的作用.
(1)实验室备有的定值电阻R.有以下几种规格:
A.10Ω,2.5W B.100Ω,1.0W C.200Ω,1.OW D.2000Ω,5.OW
本实验应选哪一种规格?答:
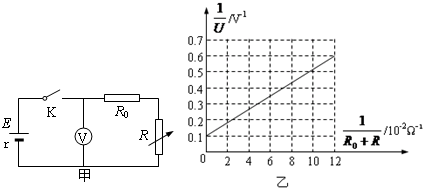
(2)该同学接人符合要求的R.后,闭合开关S,调整电阻箱的阻值,读取电压表的示数改变电阻箱阻值,取得多组数据,作出了如图(b)所示的图线(已知该直线的截距为0.1V -1).则根据该同学所作出的图线可求得该电池的电动势E为 V,内阻r为 Ω.
(1)实验室备有的定值电阻R.有以下几种规格:
A.10Ω,2.5W B.100Ω,1.0W C.200Ω,1.OW D.2000Ω,5.OW
本实验应选哪一种规格?答:

(2)该同学接人符合要求的R.后,闭合开关S,调整电阻箱的阻值,读取电压表的示数改变电阻箱阻值,取得多组数据,作出了如图(b)所示的图线(已知该直线的截距为0.1V -1).则根据该同学所作出的图线可求得该电池的电动势E为
分析:(1)已知电源电动势、内阻及最大电流,由闭合电路欧姆定律可得出电路中最小电阻,则可找出保护电阻;
(2)由闭合电路欧姆定律可得出表达式,再结合图象和数学知识可得出图象的截距及斜率的含义,则可求得电动势和内电阻.
(2)由闭合电路欧姆定律可得出表达式,再结合图象和数学知识可得出图象的截距及斜率的含义,则可求得电动势和内电阻.
解答:解:(1)当滑动变阻器短路时,电路中通过的最大电流为50mA,
则由闭合电路欧姆定律可知,定值电阻的最小阻值为:R0=
-50Ω=180-50Ω=130Ω,
滑动变阻器应选C、200Ω,1.OW;
(2)由闭合电路欧姆定律可得:U=
(R0+R),
变形得:
=
+
,
由数学知识可知,图象中的斜率k=
;截距b=
;
由图可知,b=0.1,故E=10V;
k=
=4.167;即
=4.167;
解得:r=41.67Ω;
故答案为:(1)C;(2)10;41.67.
则由闭合电路欧姆定律可知,定值电阻的最小阻值为:R0=
| E |
| I |
滑动变阻器应选C、200Ω,1.OW;
(2)由闭合电路欧姆定律可得:U=
| E |
| R0+R+r |
变形得:
| 1 |
| U |
| 1 |
| E |
| r |
| E |
| 1 |
| R+R0 |
由数学知识可知,图象中的斜率k=
| r |
| E |
| 1 |
| E |
由图可知,b=0.1,故E=10V;
k=
| 0.6-0.1 |
| 12×10-2 |
| r |
| E |
解得:r=41.67Ω;
故答案为:(1)C;(2)10;41.67.
点评:本题关键在于能由图象知识(斜率与截距的意义)结合闭合电路欧姆定律求解,在解题时要注意题目中给出的条件及坐标中隐含的信息.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
 (2)(7分)现有一种特殊的电池,它的电动势E为9V左右,内阻r大约为40Ω,为了测定这个电池的电动势和内阻,某同学利用如图2甲所示的电路进行实验,图中电压表的量程为6V,内阻为2KΩ,R1为电阻箱,阻值范围0~999Ω,R0为定值电阻.
(2)(7分)现有一种特殊的电池,它的电动势E为9V左右,内阻r大约为40Ω,为了测定这个电池的电动势和内阻,某同学利用如图2甲所示的电路进行实验,图中电压表的量程为6V,内阻为2KΩ,R1为电阻箱,阻值范围0~999Ω,R0为定值电阻.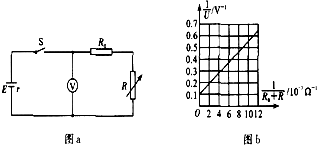
 现有一种特殊的电池,它的电动势E恒定,内阻r较大.为了测定这个电池的电动势和内电阻,某同学利用如图甲所示的电路进行实验,图中电压表的内阻很大,对电路的影响可不考虑,R为电阻箱,改变电阻箱的阻值,记录电压表示数,得到如图乙所示图线.
现有一种特殊的电池,它的电动势E恒定,内阻r较大.为了测定这个电池的电动势和内电阻,某同学利用如图甲所示的电路进行实验,图中电压表的内阻很大,对电路的影响可不考虑,R为电阻箱,改变电阻箱的阻值,记录电压表示数,得到如图乙所示图线.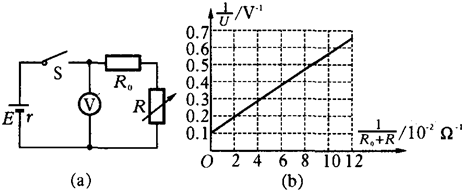 现有一种特殊的电池,电动势E约为9V,内阻r约为50Ω,允许输出的最大电流为50mA,用如图(a)的电路测量它的电动势和内阻,图中电压表的内阻非常大,R为电阻箱,阻值范围0~9999Ω.
现有一种特殊的电池,电动势E约为9V,内阻r约为50Ω,允许输出的最大电流为50mA,用如图(a)的电路测量它的电动势和内阻,图中电压表的内阻非常大,R为电阻箱,阻值范围0~9999Ω.