题目内容
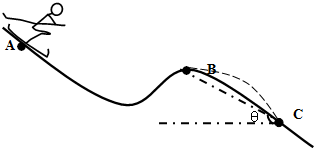 (2013?玉林模拟)如图所示,质量为m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,然后由B点水平飞出,落在斜坡上的C点.已知BC连线与水平方向的夹角θ=37°,AB间的高度差H=25m,BC两点距离S=75m,不计空气阻力.
(2013?玉林模拟)如图所示,质量为m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,然后由B点水平飞出,落在斜坡上的C点.已知BC连线与水平方向的夹角θ=37°,AB间的高度差H=25m,BC两点距离S=75m,不计空气阻力.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)运动员从B点飞出时的速度大小;
(2)运动员从A滑到B的过程中克服摩擦阻力所做的功.
分析:(1)B到C是一个平抛运动,运用平抛运动的规律解决问题,其中高度决定时间,通过水平方向运动求出初速度.
(2)运动员从A点到B点的过程中克服摩擦力做的功,由于不清楚摩擦力的大小以及A到B得位移,从功的定义式无法求解,所以我们就应该选择动能定理.
(2)运动员从A点到B点的过程中克服摩擦力做的功,由于不清楚摩擦力的大小以及A到B得位移,从功的定义式无法求解,所以我们就应该选择动能定理.
解答:解:(1)B点平抛,根据平抛运动分位移公式,有:
Scos37°=vBt--------①
Ssin370=
gt2--------②
得:vB=20m/s---------③
(2)A到B过程,由动能定理:
mgH-wf=
m
---------④
解得wf=3000J
答:(1)运动员从B点飞出时的速度大小为20m/s;
(2)运动员从A滑到B的过程中克服摩擦阻力所做的功为3000J.
Scos37°=vBt--------①
Ssin370=
| 1 |
| 2 |
得:vB=20m/s---------③
(2)A到B过程,由动能定理:
mgH-wf=
| 1 |
| 2 |
| v | 2 B |
解得wf=3000J
答:(1)运动员从B点飞出时的速度大小为20m/s;
(2)运动员从A滑到B的过程中克服摩擦阻力所做的功为3000J.
点评:解决平抛运动的问题思路是分解,即研究水平方向的匀速直线运动和竖直方向的自由落体.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.
动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

练习册系列答案
相关题目
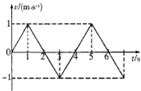 (2013?玉林模拟)某质点的运动图象如图所示,则质点( )
(2013?玉林模拟)某质点的运动图象如图所示,则质点( )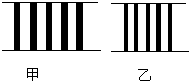 (2013?玉林模拟)a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )
(2013?玉林模拟)a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是( )