题目内容
 如图所示,水平拉力作用下,质量为m的物体A向右运动,质量为m的物体B与水平面间的动摩擦因数为u,A与水平间的摩擦,绳子与定滑轮间的摩擦不计,定滑轮的大小忽略不计.
如图所示,水平拉力作用下,质量为m的物体A向右运动,质量为m的物体B与水平面间的动摩擦因数为u,A与水平间的摩擦,绳子与定滑轮间的摩擦不计,定滑轮的大小忽略不计.(1)若图示时刻A物体的速度为v,绳子与水平向右方向的夹角为θ,求物体B的速度.
(2)若图示时刻,物体A向右加速运动,物体A的加速度为a,绳子与水平向右方向的夹角为θ,水平拉力大小为F,求物体B的加速度.
(3)若物体A在恒力F的作用下以速度为v向右匀速运动,一段时间内B向右运动一段距离,绳子与水平向右的夹角从θ1变为θ2,设A、B的高度差为H,求此过程中物体B克服摩擦力做的功.
分析:(1)根据运动的分解,可将物体B的运动沿绳子收缩的方向与转动的方向进行分解.从而运用数学知识求出物体B的速度;
(2)对物体A受力分析,由加速度可求出拉物体A的绳子拉力;再对物体B受力分析,求出其合力,从而由牛顿第二定律可求出物体B的加速度;
(3)根据运动的分解,可由物体A的运动速度可求出物体B在不同位置的速度,再由动能定理可求出此过程中物体B克服摩擦力做的功.
(2)对物体A受力分析,由加速度可求出拉物体A的绳子拉力;再对物体B受力分析,求出其合力,从而由牛顿第二定律可求出物体B的加速度;
(3)根据运动的分解,可由物体A的运动速度可求出物体B在不同位置的速度,再由动能定理可求出此过程中物体B克服摩擦力做的功.
解答:解:(1)由题意,物体B在绳子的作用下沿水平方向运动,可将其运动分解成沿绳子收缩的方向与转动的方向.
则有
由三角函数可知,vB=
(2)对物体A,重力、支持力、水平拉力与绳子的拉力
由牛顿第二定律可得:F-F绳=ma
解之得:F绳=F-ma
对物体B,受力分析:重力、支持力、绳子拉力与滑动摩擦力

将绳子的拉力进行正交分解,则由牛顿第二定律可得:
F绳cosθ-f=maB
而f=μFN
FN=F支=mg-F绳sinθ
由上可得:aB=
(3)绳子与水平向右的夹角从θ1变为θ2过程中,对物体B由动能定理可得:
F(
-
)-Wf=
m(
) 2-
m(
)2
解得:
Wf=F(
-
)-
m(
)2+
m(
)2
答:(1)若图示时刻A物体的速度为v,绳子与水平向右方向的夹角为θ,求物体B的速度vB=
;
(2)若图示时刻,物体A向右加速运动,物体A的加速度为a,绳子与水平向右方向的夹角为θ,水平拉力大小为F,求物体B的加速度aB=
;
(3)若物体A在恒力F的作用下以速度为v向右匀速运动,一段时间内B向右运动一段距离,绳子与水平向右的夹角从θ1变为θ2,设A、B的高度差为H,求此过程中物体B克服摩擦力做的功Wf=F(
-
)-
m(
)2+
m(
)2.
则有

由三角函数可知,vB=
| v |
| cosθ |
(2)对物体A,重力、支持力、水平拉力与绳子的拉力
由牛顿第二定律可得:F-F绳=ma
解之得:F绳=F-ma
对物体B,受力分析:重力、支持力、绳子拉力与滑动摩擦力

将绳子的拉力进行正交分解,则由牛顿第二定律可得:
F绳cosθ-f=maB
而f=μFN
FN=F支=mg-F绳sinθ
由上可得:aB=
| (F-ma)(cosθ+μsinθ)-μmg |
| m |
(3)绳子与水平向右的夹角从θ1变为θ2过程中,对物体B由动能定理可得:
F(
| H |
| sinθ1 |
| H |
| sinθ2 |
| 1 |
| 2 |
| v |
| cosθ2 |
| 1 |
| 2 |
| v |
| cosθ1 |
解得:
Wf=F(
| H |
| sinθ1 |
| H |
| sinθ2 |
| 1 |
| 2 |
| v |
| cosθ2 |
| 1 |
| 2 |
| v |
| cosθ1 |
答:(1)若图示时刻A物体的速度为v,绳子与水平向右方向的夹角为θ,求物体B的速度vB=
| v |
| cosθ |
(2)若图示时刻,物体A向右加速运动,物体A的加速度为a,绳子与水平向右方向的夹角为θ,水平拉力大小为F,求物体B的加速度aB=
| (F-ma)(cosθ+μsinθ)-μmg |
| m |
(3)若物体A在恒力F的作用下以速度为v向右匀速运动,一段时间内B向右运动一段距离,绳子与水平向右的夹角从θ1变为θ2,设A、B的高度差为H,求此过程中物体B克服摩擦力做的功Wf=F(
| H |
| sinθ1 |
| H |
| sinθ2 |
| 1 |
| 2 |
| v |
| cosθ2 |
| 1 |
| 2 |
| v |
| cosθ1 |
点评:除让学生掌握牛顿第二定律与动能定理外,还要学会对研究对象正确的受力分析,对运动进行合理的分解.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目

 ,求物体B的速度。
,求物体B的速度。 变为
变为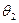 , 设A、B的高度差为H,求此过程中物体B克服摩擦力做的功。
, 设A、B的高度差为H,求此过程中物体B克服摩擦力做的功。 
 ,求物体B的速度。
,求物体B的速度。 变为
变为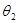 , 设A、B的高度差为H,求此过程中物体B克服摩擦力做的功。
, 设A、B的高度差为H,求此过程中物体B克服摩擦力做的功。 
