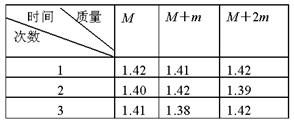
题目内容

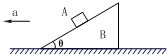质量为m的物体A与倾角为θ的斜面体B一起以共同的加速度a沿水平面向左作匀加速直线运动，以下说法正确的是（　　）
分析：将加速度沿斜面和垂直于斜面方向正交分解，通过对A的受力分析，利用牛顿第二定律求解
解答：解：A、对A受力分析，由牛顿第二定律可知：
mgtanθ=ma
a=gtanθ
此时恰好无摩擦力，故A正确
FNcosθ=mg
FN=
mg
cosθ
故D正确
B、若a＞gtanθ，设B对A的摩擦力沿斜面向上
通过受力分析，由牛顿第二定律：
mgsinθ-f=ma′
a′=acosθ＞gsinθ
联立解得：
f＜0
说明与规定的方向相反，故B错误，C正确
故选ACD
点评：本题考查灵活运用正交分解处理物理问题的能力，采用的是分解加速度，不是分解要求的力的方法，使解题过程简洁方便
练习册系列答案
相关题目
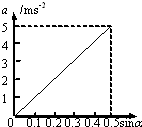某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关．实验室提供如下器材：
（A）表面光滑的长木板（长度为L），
（B）小车，
（C）质量为m的钩码若干个，
（D）方木块（备用于垫木板），
（E）米尺，
（F）秒表．
（1）实验过程：
次数/时间/质量 M M+m M+2m
1 1.42 1.41 1.42
2 1.40 1.42 1.39
3 1.41 1.38 1.42
第一步，在保持斜面倾角不变时，探究加速度与质量的关系．
实验中，通过向小车放入钩码来改变物体质量，只要测出小车由斜面顶端滑至底端所用时间t，就可以由公式a=
2L
t2
2L
t2
求出a．某同学记录了数据如上表所示：
根据以上信息，我们发现，在实验误差范围内质量改变之后平均下滑时间
不改变
不改变
（填“改变”或“不改变”），经过分析得出加速度与质量的关系为
斜面倾角一定时，加速度与物体质量无关
斜面倾角一定时，加速度与物体质量无关
．
第二步，在物体质量不变时，探究加速度与倾角的关系．实验中通过改变方木块垫放位置来调整长木板的倾角，由于没有量角器，因此通过测量出木板顶端到水平面高度h，求出倾 角α的正弦值sinα=h/L．某同学记录了高度和加速度的对应值，并在坐标纸上建立适当的坐标轴后描点作图如下，请根据他所作的图线求出当地的重力加速度g=
10
10
m/s2．进一步分析可知，光滑斜面上物体下滑的加速度与倾角的关系为
a=gsinα
a=gsinα
．

某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关。实验室提供如下器材：

（A）表面光滑的长木板（长度为L），

（B）小车，

（C）质量为m的钩码若干个，

（D）方木块（备用于垫木板），

（E）米尺，

（F）秒表。

（1）实验过程：

第一步，在保持斜面倾角不变时，探究加速度与质量的关系。

实验中，通过向小车放入钩码来改变物体质量，只要测出小车由斜面顶端滑至底端所用时间t，就可以由公式a＝__________求出a。某同学记录了数据如上表所示：

根据以上信息，我们发现，在实验误差范围内质量改变之后平均下滑时间__________（填“改变”或“不改变”），经过分析得出加速度与质量的关系为__________。

第二步，在物体质量不变时，探究加速度与倾角的关系。实验中通过改变方木块垫放位置来调整长木板的倾角，由于没有量角器，因此通过测量出木板顶端到水平面高度h，求出倾 角a的正弦值sina＝h/L。某同学记录了高度和加速度的对应值，并在坐标纸上建立适当的坐标轴后描点作图如下，请根据他所作的图线求出当地的重力加速度g＝__________m/s2。进一步分析可知，光滑斜面上物体下滑的加速度与倾角的关系为__________。

 

某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关。实验室提供如下器材：

（A）表面光滑的长木板（长度为L），

（B）小车，

（C）质量为m的钩码若干个，

（D）方木块（备用于垫木板），

（E）米尺，

（F）秒表。

（1）实验过程：

第一步，在保持斜面倾角不变时，探究加速度与质量的关系。

实验中，通过向小车放入钩码来改变物体质量，只要测出小车由斜面顶端滑至底端所用时间t，就可以由公式a＝__________求出a。某同学记录了数据如上表所示：

根据以上信息，我们发现，在实验误差范围内质量改变之后平均下滑时间__________（填“改变”或“不改变”），经过分析得出加速度与质量的关系为__________。

第二步，在物体质量不变时，探究加速度与倾角的关系。实验中通过改变方木块垫放位置来调整长木板的倾角，由于没有量角器，因此通过测量出木板顶端到水平面高度h，求出倾 角a的正弦值sina＝h/L。某同学记录了高度和加速度的对应值，并在坐标纸上建立适当的坐标轴后描点作图如下，请根据他所作的图线求出当地的重力加速度g＝__________m/s2。进一步分析可知，光滑斜面上物体下滑的加速度与倾角的关系为__________。

 

某探究性学习小组欲探究光滑斜面上物体的加速度与物体质量及斜面倾角是否有关。实验室提供如下器材：

（A）表面光滑的长木板（长度为L），

（B）小车，

（C）质量为m的钩码若干个，

（D）方木块（备用于垫木板），

（E）米尺，

（F）秒表。

（1）实验过程：

第一步，在保持斜面倾角不变时，探究加速度与质量的关系。

实验中，通过向小车放入钩码来改变物体质量，只要测出小车由斜面顶端滑至底端所用时间t，就可以由公式a＝__________求出a。某同学记录了数据如上表所示：

根据以上信息，我们发现，在实验误差范围内质量改变之后平均下滑时间__________（填“改变”或“不改变”），经过分析得出加速度与质量的关系为__________。

第二步，在物体质量不变时，探究加速度与倾角的关系。实验中通过改变方木块垫放位置来调整长木板的倾角，由于没有量角器，因此通过测量出木板顶端到水平面高度h，求出倾 角a的正弦值sina＝h/L。某同学记录了高度和加速度的对应值，并在坐标纸上建立适当的坐标轴后描点作图如下，请根据他所作的图线求出当地的重力加速度g＝__________m/s2。进一步分析可知，光滑斜面上物体下滑的加速度与倾角的关系为__________。
如图所示，质量为m的物体沿倾 角为θ的斜面匀速下滑，物体与斜面间的动摩擦因数为μ，关于物体在下滑过程中所受滑动摩擦力的大小Ff，下列说法正确的是
①Ff = mgsinθ ②Ff = mgcosθ ③Ff = μmgsinθ ④Ff=μmgcosθ

[     ]

A．①②
B．②③
C．①③
D．①④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网