题目内容
13. 两块金属板a、b平行放置,板长l=10cm,两板间距d=3.0cm,在a、b两板间同时存在着匀强电场和与电场正交的匀强磁场,磁感应强度B=2.5×10-4T.一束电子以一定的初速度v0=2.0×107m/s从两极板中间沿垂直于电场、磁场的方向射入场中,并沿着直线通过场区,如图所示.已知电子电荷量e=-1.6×10-19C,质量m=0.91×10-30kg.
两块金属板a、b平行放置,板长l=10cm,两板间距d=3.0cm,在a、b两板间同时存在着匀强电场和与电场正交的匀强磁场,磁感应强度B=2.5×10-4T.一束电子以一定的初速度v0=2.0×107m/s从两极板中间沿垂直于电场、磁场的方向射入场中,并沿着直线通过场区,如图所示.已知电子电荷量e=-1.6×10-19C,质量m=0.91×10-30kg.(1)求a、b两板间的电势差U为多大.
(2)若撤去磁场,求电子离开电场时偏离入射方向的距离.
(3)若撤去磁场,求电子通过电场区增加的动能.
分析 (1)根据洛伦兹力与电场力平衡,结合公式E=$\frac{U}{d}$,即可求解;
(2)根据运动学公式与牛顿第二定律,即可求解;
(3)根据动能定理,即可求解.
解答 解:(1)电子进入正交的电磁场不发生偏转,洛伦兹力与电场力平衡,
则有:ev0B=eE,又:E=$\frac{U}{d}$,解得:U=150V;
(2)电子在电场中做匀变速曲线运动,设电子通过场区的时间为t,偏转的距离为y,则
水平方向:l=v0t,竖直方向:由牛顿第二定律得:a=$\frac{eU}{md}$,位移:y=$\frac{1}{2}$at2,解得:y=1.1×10-2m
(3)因电子通过电场时只有电场力做功,由动能定理得:△Ek=eEy,解得:△Ek=8.8×10-18J
答:(1)则a、b两板间的电势差U为150V.
(2)若撤去磁场,则电子穿过电场偏离入射方向的距离1.1×10-2m.
(3)则撤去磁场后,电子通过电场区增加的动能8.8×10-18J.
点评 本题考查运动学公式与牛顿第二定律的应用,掌握动能定理的运用,知道洛伦兹力与电场力的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.一物块置于水平地面上,在20N水平拉力作用下向前移动了6m,水平拉力对物块所做的功是( )
| A. | 80J | B. | 100J | C. | 120J | D. | 200J |
8. 如图所示,电路中的变压器为理想变压器,S为单刀双掷开关,P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I0、I1分别为原线圈和副线圈中的电流,下列说法正确的是( )
如图所示,电路中的变压器为理想变压器,S为单刀双掷开关,P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I0、I1分别为原线圈和副线圈中的电流,下列说法正确的是( )
 如图所示,电路中的变压器为理想变压器,S为单刀双掷开关,P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I0、I1分别为原线圈和副线圈中的电流,下列说法正确的是( )
如图所示,电路中的变压器为理想变压器,S为单刀双掷开关,P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I0、I1分别为原线圈和副线圈中的电流,下列说法正确的是( )| A. | 保持P的位置及U不变,S由b切换到a,则R上消耗的功率减小 | |
| B. | 保持P的位置及U不变,S由a切换到b,则I1减小 | |
| C. | 保持P的位置及U不变,S由b切换到a,则I1增大 | |
| D. | 保持U不变,S接b端,将P向上滑动,则I1减小 |
18.假设飞机在飞行中所受空气阻力与它的速度平方成正比,当飞机以速度v水平匀速飞行时,发动机的功率为P,若飞机以速度3v水平飞行时,发动机的功率为( )
| A. | 3P | B. | 9P | C. | 18P | D. | 27 P |
5.关于热量、功和内能三个物理量,下列说法中正确的是( )
| A. | 热量、功都可以作为物体内能变化的量度 | |
| B. | 功由过程决定,而热量和内能由物体的状态决定 | |
| C. | 热量、功和内能三者的物理意义相同,只是说法不同 | |
| D. | 热量、功和内能的单位不同 |
3. 在竖直向上的拉力F作用下,将货物由地面吊起,其运动的v2-x图象如图所示(取g=10m/s2).则前3m内与最后2m内拉力的大小之比( )
在竖直向上的拉力F作用下,将货物由地面吊起,其运动的v2-x图象如图所示(取g=10m/s2).则前3m内与最后2m内拉力的大小之比( )
 在竖直向上的拉力F作用下,将货物由地面吊起,其运动的v2-x图象如图所示(取g=10m/s2).则前3m内与最后2m内拉力的大小之比( )
在竖直向上的拉力F作用下,将货物由地面吊起,其运动的v2-x图象如图所示(取g=10m/s2).则前3m内与最后2m内拉力的大小之比( )| A. | 12:7 | B. | 22:17 | C. | 22:23 | D. | 18:23 |
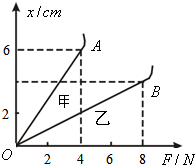 在“探究弹力与弹簧伸长的关系”的实验中.
在“探究弹力与弹簧伸长的关系”的实验中. 如图所示电路,电阻R1=2Ω,R2=10Ω,R3=3Ω.保持S1闭合,S2接通和断开时电源的总功率之比为9:5,则电源的内电阻为0.3Ω,S2接通和断开时电流表的示数之比为9:4.
如图所示电路,电阻R1=2Ω,R2=10Ω,R3=3Ω.保持S1闭合,S2接通和断开时电源的总功率之比为9:5,则电源的内电阻为0.3Ω,S2接通和断开时电流表的示数之比为9:4. 如图,质量为2kg的木块静止在水平地面上的P点,用水平恒力F拉动,拉力F做了12J的功后撤去F,最后木块滑行到Q点停止运动,已知P、Q两点间的距离为3m,全过程所用的时间为3s,求:
如图,质量为2kg的木块静止在水平地面上的P点,用水平恒力F拉动,拉力F做了12J的功后撤去F,最后木块滑行到Q点停止运动,已知P、Q两点间的距离为3m,全过程所用的时间为3s,求: