题目内容
11. 如图所示,质量为m的物体与A、B两个弹簧相连,B弹簧下端与地相连,A、B劲度系数分别为k1和k2.现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{2}{3}$时,且弹簧B仍处于收缩状态,A上端移动的距离是多少?
如图所示,质量为m的物体与A、B两个弹簧相连,B弹簧下端与地相连,A、B劲度系数分别为k1和k2.现用手拉A的上端,使A缓慢上移,当B弹簧的弹力为原来的$\frac{2}{3}$时,且弹簧B仍处于收缩状态,A上端移动的距离是多少?
分析 B原来处于压缩状态,后来仍处于压缩状态,根据胡克定律分别求出B原来压缩量和后来的压缩量,即可得到物体上移的距离.再根据胡克定律求出弹簧A的伸长量,加上m上移的距离就是A端上移的距离.
解答 解:B弹簧原先处于压缩状态,其压缩量为:x0=$\frac{mg}{{k}_{2}}$,A弹簧无形变.
当向上缓慢拉住弹簧A的上端,缓慢上移,使B弹簧的弹力为原来的$\frac{2}{3}$时,且弹簧B仍处于收缩状态,此时A弹簧的弹力和伸长量分别为
F1=mg-F2=mg-$\frac{2}{3}$mg=$\frac{1}{3}$mg,
x1=$\frac{{F}_{1}}{{k}_{1}}$=$\frac{mg}{3{k}_{1}}$
这时B上端的位移为:x2=$\frac{△{F}_{2}}{{k}_{2}}$=$\frac{\frac{1}{3}mg}{{k}_{2}}$=$\frac{mg}{3{k}_{2}}$
所以A的上端上移距离为:S1=x1+x2=$\frac{1}{3}$mg($\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$);
答:A上端移动的距离是 $\frac{1}{3}$mg($\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$).
点评 本题的解题关键是分析弹簧的状态,分析出A端上移的距离与弹簧形变量的关系,结合几何关系研究.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
13.下列所列数据不属于交流电有效值的是( )
| A. | 交流电表的示数 | B. | 电容器的耐压值 | ||
| C. | 灯泡的额定电压 | D. | 保险丝的额定电流 |
2. 如图所示,质量为m1的木块受到向右的拉力F的作用,使之在m2的长木板上向右滑行,长木板始终保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,则( )
如图所示,质量为m1的木块受到向右的拉力F的作用,使之在m2的长木板上向右滑行,长木板始终保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,则( )
 如图所示,质量为m1的木块受到向右的拉力F的作用,使之在m2的长木板上向右滑行,长木板始终保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,则( )
如图所示,质量为m1的木块受到向右的拉力F的作用,使之在m2的长木板上向右滑行,长木板始终保持静止状态.已知木块与长木板间的动摩擦因数为μ1,长木板与地面间的动摩擦因数为μ2,则( )| A. | 长木板受到地面的摩擦力大小一定为μ2(m1+m2)g | |
| B. | 由整体法可知长木板受到地面的摩擦力大小一定为F | |
| C. | 无论怎样改变F的大小,长木板都不可能运动 | |
| D. | 增大F的大小,长木板可能会运动 |
19.科学家在“哥伦比亚”号航天飞机上进行了一次在微重力条件(即失重状态)下制造泡沫金属的实验.把锂、镁、铝、钛等轻金属放在一个石英瓶内,用太阳能将这些金属融化成液体,然后在融化的金属中冲进氢气,使金属内产生大量气泡,金属冷凝后就形成到处是微孔的泡沫金属.下列说法正确的是( )
| A. | 泡沫金属物理性质各向异性,说明它是非晶体 | |
| B. | 失重条件下液态金属呈现球状是由于液体表面分子间只存在引力 | |
| C. | 在金属冷凝过程中,气泡收缩变小,外界对气体做功,气体内能增加 | |
| D. | 在失重条件下充入金属液体内的气体不能无限膨胀是由于液体表面张力的约束 |
16.天花板上电线悬吊电灯的情形中,下列各对力中属于作用力和反作用力的是( )


| A. | 电灯受到的重力和电线对电灯的拉力 | |
| B. | 电线对电灯的拉力和电灯对电线的拉力 | |
| C. | 电线对电灯的拉力和天花板对电线的拉力 | |
| D. | 电灯受到的重力和电灯对电线的拉力 |
3.下列关于运动和力的关系的认识符合物理学史实的是( )
| A. | 亚里士多德认为,力是改变物体运动状态的原因 | |
| B. | 牛顿认为,物体间的作用力和反作用力总是大小相等,方向相反,合力为零 | |
| C. | 伽利略认为重的物体下落得快,轻的物体下落得慢 | |
| D. | 笛卡儿指出:如果运动中的物体没有受到力的作用,它将继续以同一速度沿同一直线运动,既不停下来也不偏离原来的方向 |
20.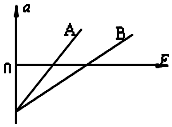 如图所示,A、B两条直线是在A、B两地分别用竖直向上的力F去拉质量分别为mA和mB的两个物体得出的加速度a与拉力F之间的关系图线,由图线可知( )
如图所示,A、B两条直线是在A、B两地分别用竖直向上的力F去拉质量分别为mA和mB的两个物体得出的加速度a与拉力F之间的关系图线,由图线可知( )
 如图所示,A、B两条直线是在A、B两地分别用竖直向上的力F去拉质量分别为mA和mB的两个物体得出的加速度a与拉力F之间的关系图线,由图线可知( )
如图所示,A、B两条直线是在A、B两地分别用竖直向上的力F去拉质量分别为mA和mB的两个物体得出的加速度a与拉力F之间的关系图线,由图线可知( )| A. | 两地的重力加速度gA=gB | B. | 两地的重力加速度gA>gB | ||
| C. | 两物体的质量mA>mB | D. | 两物体的质量mA<mB |
1.某同学站在匀速上升的电梯内,已知该同学体重为600N,在电梯减速直至停止的过程中,以下说法正确的是(g取10m/s2)( )
| A. | 该同学体重仍为600 N | B. | 该同学体重小于600 N | ||
| C. | 该同学对电梯地板压力大于600 N | D. | 该同学对电梯地板压力小于600 N |