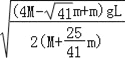题目内容
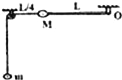
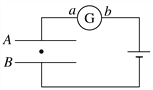
【题目】如图所示,竖直光滑直轨道OA高度为2R,连接半径为R的半圆形光滑环形管道ABC(B为最低点),其后连接![]() 圆弧环形粗糙管道CD,半径也为R.一个质量为m的小球从O点由静止释放,自由下落至A点进入环形轨道,从D点水平飞出,下落高度刚好为R时,垂直落在倾角为30°的斜面上P点,不计空气阻力,重力加速度为g.求:
圆弧环形粗糙管道CD,半径也为R.一个质量为m的小球从O点由静止释放,自由下落至A点进入环形轨道,从D点水平飞出,下落高度刚好为R时,垂直落在倾角为30°的斜面上P点,不计空气阻力,重力加速度为g.求:
(1)小球运动到B点时对轨道的压力大小;
(2)小球运动到D点时的速度大小;
(3)小球在环形轨道中运动时,摩擦力对小球做了多少功?

【答案】(1)N =7mg(2)![]() (3)-
(3)-![]() mgR
mgR
【解析】(1)O→B:3mgR=![]() mυB2
mυB2
B点:N– mg=m![]()
N ˊ= N =7mg
(2)D→P:υy=gt R=![]() gt2
gt2
在P点:![]() =tan60°
=tan60°
υD=![]()
(3)O→D:mgR+Wf =![]() mυD2 Wf =-
mυD2 Wf =-![]() mgR
mgR
本题综合考查了曲线运动,根据牛顿第二定律可得小球在B点时对轨道的压力,要求小球在D点时的速度,可把运动过程逆过来球,现根据小球做平抛运动的规律求出平抛运动的初速度,即D点的速度从O到D整个过程中只有重力和摩擦力做功,可根据动能定理求得。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目