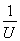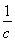题目内容
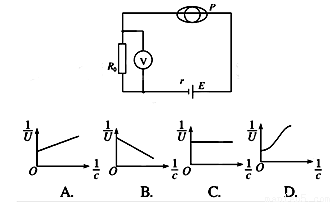
如图所示，一质量不计的轻质弹簧的上端与盒子A连接在一起，盒子A放在倾角为θ=300的光滑固定斜面上,下端固定在斜面上.盒子内装一个光滑小球，盒子内腔为正方体，一直径略小于此正方形边长的金属圆球B恰好能放在盒内，已知弹簧劲度系数为k=100N/m，盒子A和金属圆球B质量均为1kg.，将A沿斜面向上提起，使弹簧从自然长度伸长10cm，从静止释放盒子A，A和B一起在斜面上做简谐振动，g取10m/s2，求：
（1）盒子A的振幅.
（2）金属圆球B的最大速度.
（3）盒子运动到最低点和最高点时，盒子A对金属圆球B的作用力大小
(1) 20cm（2）1.4m/s（3）5N
【解析】
试题分析：(1) 振子在平衡位置时，所受合力为零，
设此时弹簧被压缩Δx
／
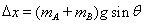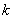=10cm
释 放 时振子处在最大位移处，故振幅A为： A=10cm+10cm=20cm
(2) 由于开始时弹簧的伸长量恰等于振子在平衡位置时弹簧的压缩量，
故弹簧势能相等，设振子的最大速率为v，
从开始到平衡位置，根据机械能守恒定律：
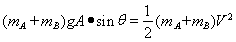
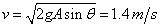
(3)在最低点，振子受到的重力分力和弹力方向相反，根据牛顿第二定律:
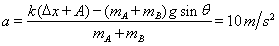
A对B的作用力方向向上，其大小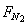
为：
=
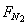=15N
在最高点振子受到的重力分力和弹力方向相同，根据牛顿第二定律：
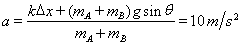(或由对称性可得)
A对B的作用力方向向下，其大小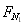
为：
=
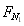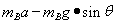=5N
考点：弹簧振子简谐振动 牛顿第二定律
下表列出了某品牌电动自行车及所用电动机的主要技术参数，不计其自身机械损耗。若该车在额定状态下以最大运行速度行驶，则 ( )
自重 | 40 kg | 额定电压 | 48 V |
载重 | 75 kg | 额定电流 | 12 A |
最大行驶速度 | 36 km/h | 额定输出功率 | 350 W |
A．电动机的输入功率为576 W B．电动机的内电阻为4 Ω
C．该车获得的牵引力为57.6 N D．该车受到的阻力为35 N
