题目内容

如图所示，中子内有一个电荷量为+
2
3
e的上夸克和两个电荷量为-
1
3
e的下夸克，3个夸克都分布在半径为 r 的同一圆周上，则3个夸克在其圆心处产生的电场强度为（　　）
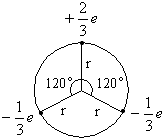
分析：先将两个电荷量为-
1
3
e的下夸克在圆心处产生的电场强度进行合成，再与电荷量为+
2
3
e的上夸克在圆心处产生的电场强度合成，求出3个夸克在其圆心处产生的电场强度．
解答：解：一个下夸克在圆心处产生的电场强度大小为E1=k
1
3
e
r2
=
ke
3r2
，两个电荷量为-
1
3
e的下夸克在圆心处产生的合场强大小为E2=E1=
ke
3r2
，方向沿A→O．电荷量为+
2
3
e的上夸克在圆心处产生的电场强度大小为E3=k
2
3
e
r2
=
2ke
3r2
，方向沿A→O，所以3个夸克在其圆心处产生的电场强度大小E=E2+E3=
ke
r2
，方向沿A→O．
故选A
点评：本题电场的叠加问题，要利用对称性．对于两个下夸克场强的合成可利用力的合成进行类比．
练习册系列答案
相关题目
（2004?天津）中子内有一个电荷量为
+2e
3
的上夸克和两个电荷量为
-e
3
的下夸克，一简单模型是三个夸克都在半径为r的同一圆周，如图所示．下图给出的四幅图中，能正确表示出各夸克所受静电作用力的是（　　）
（2011?湖南一模）[物理选修3-5模块]
（1）下列说法中正确的是
AD
AD
．
A．卢瑟福通过实验发现了质子的核反应方程为24He+714N→817O+11H
B．铀核裂变的核反应是：92235U→56141Ba+3692Kr+201n
C．质子、中子、α粒子的质量分别为m1、m2、m3．质子和中子结合成一个α粒子，释放的能量是：（m1+m2-m3）c2
D．原子从a能级状态跃迁到b能级状态时发射波长为λ1的光子；原子从b能级状态跃迁到c能级状态时吸收波长为λ2的光子，已知λ1＞λ2．那么原子从a能级状态跃迁到c能级状态时将要吸收波长为
λ1λ2λ1-λ2
的光子
（2）如图所示，质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端栓在固定挡板P上，另一端与靶盒A连接．Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度为v0=50m/s，质量m=0.010kg的弹丸，当弹丸打入靶盒A后，便留在盒内，碰撞时间极短．不计空气阻力．求弹丸进入靶盒A后，弹簧的最大弹性势能为多少？
[物理--选修3-5]
（1）北京时间2011年3月11日13时46分，在日本本州岛附近海域发生里氏9.0级强烈地震，地震和海啸引发福岛第一核电站放射性物质泄漏，其中放射性物质碘131的衰变方程为13153I→13154Xe+Y．根据有关放射性知识，下列说法正确的是
A
A

A．Y粒子为β粒子
B．13153I的半衰期大约是8天，则若取4个碘原子核，经16天就一定剩下1个碘原子核了
C．生成的13154Xe处于激发态，还会放射γ射线．γ射线的穿透能力最强，电离能力也最强
D．13153I中有53个质子和131个中子
（2）如图所示，两光滑圆轨道放置在同一竖直平面内，半径均为R，两轨道之间由一光滑水平轨道相连，在水平轨道上有一轻弹簧被 a、b两个小球夹住，但不拴接．已知a小球的质量为m，b小球的质量为2m，同时释放两小球，且要求a、b都能通过两圆轨道的最高点，则弹簧在释放前至少具有多大的弹性势能？
（2010?盐城三模）本题包括A、B、C三小题，请选定其中的两题，并在相应的答题区域作答．若三题都做，则按A、B两题评分．
A．（1）以下说法正确的是的
BD
BD

A、液体中的扩散现象是由于外界对液体作用引起的．
B、多晶体沿各个方向的物理性质表现为各向同性．
C、分子间距离为平衡距离时，分子间作用力为零，分子势力能最大．
D、温度相同的物体分子平均动能一定相同，而分子无规则运动的平均速率不一定相同．
（2）给旱区人民送水的消防车停在水平地面上，在缓慢放水的过程中，若车胎不漏气，胎内气体温度不变，不计分子间作用力，则胎内
吸收
吸收
热量（填“吸收”或“放出”），单位时间内单位面积的车胎内壁受到气体分子平均撞击次数不清
减少
减少
（填“增加”、“减少”或“不变”）．
（3）标准状态下气体的摩尔体积为V0=22.4L/mol，请估算教室内空气分子的平均间距d．设教室内的温度为0℃，阿伏加德罗常数NA=6X1023mol-1，（要写出必要的推算过程，计算结果保留1位有效数字）．
B．
（1）北京时间2011年3月11日13时46分，在日本东北部宫城县以东太平洋海域发生里氏9.0级地震，地震造成了重大的人员伤亡，下列说法正确的是
BC
BC

A、震源停止振动时，地震波的传播立即停止．
B、地震波能传播能量．
C、当地震波由海底传播到海水中时地震波的频率不变．
D、地震波与电磁波一样均可以在真空中传播．
（2）图甲所示是一列沿X轴正方向传播的简谐横波在t=0时刻的波形，质点P的振动图象如图乙所示，则这列波的传播速度
2
2
m/s，质点P的振动方程为X=
8sin0.5πt
8sin0.5πt
cm．
（3）如图丙所示，一个截面为直角三角形的玻璃砖放在水平面上，折射率n=
2
．入射光线垂直于AB边从F点射入玻璃砖，经E点折射后到达地面上的P点，已知AE=ED=L，∠ABD=60°，试求光线从F到P所用时间？（光在真空中的速度大小为c）．

C．（1）核能作为一种新能源在现代社会中已不可缺少，但安全是核电站面临的非常严峻的问题．核泄漏中的钚（Pu）是一种具有放射性的超铀元素，钚的危险性在于它对人体的毒性，与其他放射性元素相比钚在这方面更强，一旦侵入人体，就会潜伏人体肺部、骨骼等组织细胞中，破坏细胞基因，提高罹患癌症的风险．已知钚的一种同位素94239Pu的半衰期为24100年，其衰变方程为94239Pu→X+24He+γ，下列有关说法正确的是
AD
AD


A、X原子核中含有143个中子．
B、100个94239Pu经过24100年后一定还剩余50个．
C、由于衰变时释放巨大能量，根据E=mC2，衰变过程总质量增加．
D、衰变发出的γ、放射线是波长很短的光子，具有很强的穿透能力．
（2）氢原子弹的光谱在可见光范围内有四条谱线，其中在靛紫色区内的一条是处于量子数n=4的能级氢原子跃迁到n=2的能级发出的，氢原子的能级如图所示，已知普朗克恒量h=6.63×10-34J?s，则该条谱线光子的能量为
2.55
2.55
eV，该条谱线光子的频率为
6.15×1014
6.15×1014
Hz．（结果保留3位有效数字）
（3）已知金属铷的极限频率为5.15×1014Hz，现用波长为5.0×10-7m的一束光照射金属铷，能否使金属铷发生光电效应？若能，请算出逸出光电子的最大初动能．（结果保留2位有效数字）

如图所示，中子内有一个电荷量为的上夸克和两个电荷量为的下夸克，3个夸克都分布在半径为 r 的同一圆周上，则3个夸克在其圆心处产生的电场强度为：

A．　　　B．          C．　　　　D．

  8．某空间内有高度为d、宽度足够宽、方向水平向左的匀强电场。当在该空间内建立如图所示的坐标系后，在x轴上的P点沿y轴正方向连续射入相同的带电粒子（粒子重力不计），由于粒子的入射速率v不同，有的粒子将在电场中直接通过y轴，有的将穿出电场后再通过y轴。设粒子通过y轴时，离坐标原点的距离为h，从P到y轴所需的时间为t，则  

           A．粒子的电势能可能增大

           B．对h≤d的粒子，h越大，t越大

           C．对h>d的粒子，h不同，在时间t内，电场力对粒子做的功不相等

           D．不同h对应的粒子，进入电场时的速率v可能相同

二、选择题（本题共4小题，每小题4分，共16分。在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。全部选对的得4分，选不全的得2分，有选错或不答的得0分。）

9．做初速不为零的匀加速直线运动的物体在时间T 内通过位移s1到达 A 点，接着在时间 T 内又通过位移 s2到达 B 点，则以下判断正确的是

    A．物体在A点的速度大小为     B．物体运动的加速度为

    C．物体运动的加速度为        D．物体在B点的速度大小为

10．如图所示，轰炸机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，并垂直击中山坡上的目标A。已知A点高度为h，山坡倾角为θ，由此可算出

   A.轰炸机的飞行高度             B.轰炸机的飞行速度

   C.炸弹击中山坡时的速度         D.炸弹投出时的动能

11.如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体接触（未连接），弹簧水平且无形变。用水平力，缓慢推动物体，在弹性限度内弹簧长度被压缩了x0，此时物体静止。撤去F后，物体开始向左运动，运动的最大距离为4x0。物体与水平面间的动摩擦因数为μ，重力加速度为g。则                   

  A．撤去F后，物体先做匀加速运动，再做匀减速运动

  B．撤去F后，物体刚运动时的加速度大小为

  C．弹簧被压缩了x0时具有的弹性势能为

  D．物体开始向左运动到速度最大的过程中克服摩擦力做的功为

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网