题目内容
19.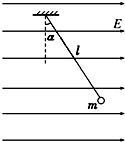 一根长为l的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直位置的偏角为α,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g),求:
一根长为l的丝线吊着一质量为m,带电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直位置的偏角为α,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g),求:(1)小球带何种电荷,匀强电场的电场强度的大小?
(3)小球经过最低点时丝线的拉力.
分析 (1)以小球为研究对象,分析受力情况,由于小球处于静止状态,合力为零,由平衡条件分析电场力的方向,求解电场强度大小;
(2)当电场方向变为向下后,小球受到的电场力竖直向下,向下做圆周运动,根据动能定理求解小球经过最低点时的瞬时速度;小球经过最低点时,由重力、电场力和丝线的拉力的合力提供了向心力,根据牛顿第二定律求解丝线对小球的拉力
解答  解:(1)由受力方向可知小球带正电
解:(1)由受力方向可知小球带正电
由于小球带正电,如图所示,由平衡条件得:mgtanα=qE
故:$E=\frac{mgtanα}{q}$
(2)电场方向变成向下后,小球开始摆动做圆周运动,重力、电场力对小球做正功.由动能定理:$(mg+qE)l(1-cosα)=\frac{1}{2}m{v^2}$
在最低点,由牛顿第二定律得: ${F_向}={F_T}-(mg+qE)=m\frac{v^2}{l}$
${F_向}={F_T}-(mg+qE)=m\frac{v^2}{l}$
由以上各式解得:FT=(mg+qE)(3-2cosα)
答:(1)小球带正电,场强E为$\frac{mgtanα}{q}$
(2)小球经过最低点时丝线的拉力为=(mg+qE)(3-2cosα)
点评 运用动能定理求速度,根据牛顿第二定律求丝线的拉力,是常用的方法和思路,要能熟练运用力学方法解决电场中的问题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
7.在研究下述运动时,能把物体看作质点的是( )
| A. | 在空中做翻腾运动的体操运动员 | |
| B. | 研究自行车车轮的旋转 | |
| C. | 研究火车从南京到上海运行需要的时间 | |
| D. | 研究奥运冠军张怡宁打出的乒乓球的旋转方向 |
14.下列物体运动过程中满足机械能守恒的是( )
| A. | 忽略空气阻力,物体竖直上抛 | |
| B. | 跳伞运动员张开伞后,在空中匀速下降 | |
| C. | 火箭升空 | |
| D. | 拉着物体沿光滑斜面匀速上升 |
11.有一未知电阻Rx,为较准确地测出其阻值,先后采用两种方法测量,用外接法测得的数据为“2.8V,5.0mA”,利用内接法测得的数据为“3.0V,4.0mA”,那么该电阻的测量值中较准确的数值及其比真实值偏大或偏小的情况分别是( )
| A. | 560Ω,偏大 | B. | 560Ω,偏小 | C. | 750Ω,偏大 | D. | 750Ω,偏小 |
8. 如图,足够长的光滑导轨倾斜放置,其下端与小灯泡连接,匀强磁场垂直于导轨所在平面,则垂直导轨的导体棒ab在下滑过程中(导体棒电阻为R,导轨和导线电阻不计)( )
如图,足够长的光滑导轨倾斜放置,其下端与小灯泡连接,匀强磁场垂直于导轨所在平面,则垂直导轨的导体棒ab在下滑过程中(导体棒电阻为R,导轨和导线电阻不计)( )
 如图,足够长的光滑导轨倾斜放置,其下端与小灯泡连接,匀强磁场垂直于导轨所在平面,则垂直导轨的导体棒ab在下滑过程中(导体棒电阻为R,导轨和导线电阻不计)( )
如图,足够长的光滑导轨倾斜放置,其下端与小灯泡连接,匀强磁场垂直于导轨所在平面,则垂直导轨的导体棒ab在下滑过程中(导体棒电阻为R,导轨和导线电阻不计)( )| A. | 受到的安培力大小保持恒定 | |
| B. | 受到的安培力方向沿斜面向上 | |
| C. | 导体棒的机械能一直减小 | |
| D. | 克服安培力做的功等于灯泡消耗的电能 |

 三个力共同作用在O点,如图,F1与F2、F2与F3之间的夹角均为60°,F1=10N,F2=20N,F3=30N.求三个力的合力.
三个力共同作用在O点,如图,F1与F2、F2与F3之间的夹角均为60°,F1=10N,F2=20N,F3=30N.求三个力的合力.