题目内容
11.沿半球形碗的光滑内表面,一个质量为m的小球正以角速度ω在水平面内做匀速圆周运动,如果碗的半径为R,则该小球做匀速圆周运动的轨道平面离碗底的高度为R-$\frac{g}{{ω}^{2}}$.分析 小球在水平面内做匀速圆周运动,靠重力和支持力的合力通过向心力,根据牛顿第二定律,结合几何关系求出球做匀速圆周运动的水平面离碗底的距离.
解答 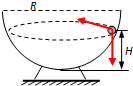 解:因为小球做的是匀速圆周运动,所以小球的向心力就是小球所受的合力,小球受重力、碗的支持力(指向球心),如下图.为保证这两个力的合力指向圆周运动的圆心(不是球心),则将支持力分解后必有竖直方向分力等于重力,水平方向分力即为向心力.设支持力与水平方向夹角为θ,
解:因为小球做的是匀速圆周运动,所以小球的向心力就是小球所受的合力,小球受重力、碗的支持力(指向球心),如下图.为保证这两个力的合力指向圆周运动的圆心(不是球心),则将支持力分解后必有竖直方向分力等于重力,水平方向分力即为向心力.设支持力与水平方向夹角为θ,
则有:F向=$\frac{mg}{tanθ}$=mω2Rcosθ
解得:sinθ=$\frac{g}{R{ω}^{2}}$.
则小球的高度为:H=R-Rsinθ=R-$\frac{g}{{ω}^{2}}$.
故答案为:R-$\frac{g}{{ω}^{2}}$.
点评 解决本题的关键知道小球做圆周运动向心力的来源,结合牛顿第二定律和几何关系进行求解.

练习册系列答案
相关题目
19.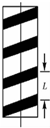 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )| A. | 顺时针 转速n=$\frac{v}{2πL}$ | B. | 顺时针 转速n=$\frac{v}{L}$ | ||
| C. | 逆时针 转速n=$\frac{v}{2πL}$ | D. | 逆时针 转速n=$\frac{v}{L}$ |
16.河宽为d,水流速度为v1,船在静水中的速度为v2,要使船在渡河过程中通过位移s最短,则下列说法正确的是( )
| A. | v1>v2时,s=d | B. | v1<v2时,s<d | C. | v1>v2时,s>d | D. | v1<v2时,s=d |
3. 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )| A. | 滑块克服摩擦力所做的功为fL | |
| B. | 上述过程满足(F-f)(L+s)=$\frac{1}{2}$mv12+$\frac{1}{2}{m}_{1}{{v}_{2}}^{2}$ | |
| C. | 其他条件不变的情况下,F越大,滑块到达右端所用时间越长 | |
| D. | 其他条件不变的情况下,f越大,滑块与木板间产生的热量越多 |
20.健身球是一个充满气体的大皮球,当人压向健身球上时,假设球内气体温度不变,则在这个过程中( )


| A. | 气体分子的平均动能增大 | B. | 气体的密度增大 | ||
| C. | 气体从外界吸收热量 | D. | 外界对气体做功 |
1.对于曲线运动,下列说法中正确的是( )
| A. | 速度方向可能不变 | B. | 加速度一定是变化 | ||
| C. | 速度方向和加速度方向不可能一致 | D. | 合外力一定与速度方向垂直 |
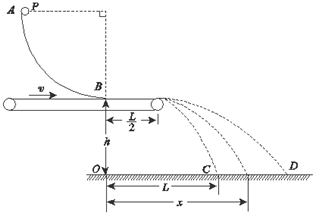 如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:
如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求: 如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.
如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.