题目内容
水平固定的两个足够长的平行光滑杆MN、PQ,两者之间的间距为L,两光滑杆上分别穿有一个质量分别为MA=0.1kg和MB=0.2kg的小球A、B,两小球之间用一根自然长度也为L的轻质橡皮绳相连接,开始时两小球处于静止状态,如图1所示.现给小球A一沿杆向右的水平速度v=6m/s,以向右为速度正方向,以小球A获得速度开始计时得到A球的v-t图象如图2所示.(以后的运动中橡皮绳的伸长均不超过其弹性限度.)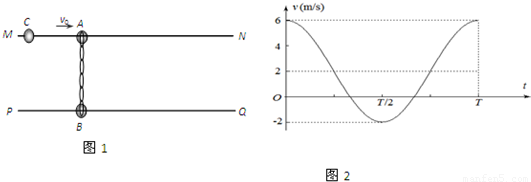
(1)在图2中画出一个周期内B球的v-t图象(不需要推导过程);
(2)若在A球的左侧较远处还有另一质量为MC=0.1kg粘性小球C,当它遇到小球A,即能与之结合在一起.某一时刻开始C球以4m/s的速度向右匀速运动,在A的速度为向右大小为2m/s时,C遇到小球A,则此后橡皮绳的最大弹性势能为多少?
(3)C球仍以4m/s的速度向右匀速运动,试定量分析在C与A相遇的各种可能情况下橡皮绳的最大弹性势能.
【答案】分析:(1)AB运动过程中动量守恒,根据动量守恒定律求出B球的几个速度值,描点连成光滑曲线即可;
(2)根据动量守恒定律求出AC共同速度,再求出碰撞损失的机械能,当三球速度相同时橡皮绳子弹性势能最大,根据能量关系求出橡皮绳的最大弹性势能;
(3)当A球在运动过程中速度为4m/s与C球同向时,C球与之相碰时系统损失能量最小(为0),橡皮绳具有的最大弹性势能,当A球在运动过程中速度为2m/s与C球反向时(此时B的速度为,C球与之相碰时系统损失能量最大,橡皮绳具有的最大弹性势能,根据能量关系求解此最大弹性势能,最后求出范围.
解答: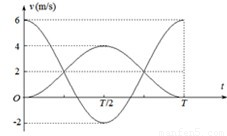 解:(1)AB运动过程中动量守恒,根据动量守恒定律得:
解:(1)AB运动过程中动量守恒,根据动量守恒定律得:
MAv=MAvA+MBvB
当vA=6m/s时vB=0
当vA=2m/s时vB=2m/s
当vA=-2m/s时vB=4m/s
所以一个周期内B球的v-t图象如图所示:
(2)AC碰撞,动量守恒:MAvA+MCvC=(MA+MC)vAC
解得:vAC=3m/s
碰撞损失的机械能为:△EK= MAvA2+
MAvA2+ MCvC2-
MCvC2- (MA+MC)vAC2=0.1J
(MA+MC)vAC2=0.1J
当三球速度相同时橡皮绳子弹性势能最大,MAv+MCvC=(MA+MB+MC)v共
解得:v共=2.5m/s
所以 EPmax= MAv2+
MAv2+ MCvC2-
MCvC2- =(MA+MB+MC)v共2-△EK
=(MA+MB+MC)v共2-△EK
解得:EPmax=1.25J
(3)①:当A球在运动过程中速度为4m/s与C球同向时,C球与之相碰时系统损失能量最小(为0),橡皮绳具有的最大弹性势能为EPmax1
EPmax1= MAv2+
MAv2+ MCvC2-
MCvC2- (MA+MB+MC)v共2=1.35J
(MA+MB+MC)v共2=1.35J
②:当A球在运动过程中速度为2m/s与C球反向时(此时B的速度为,C球与之相碰时系统损失能量最大,橡皮绳具有的最大弹性势能为EPmax2,
MCvC-MAvA=(MA+MC)v′AC
解得v′AC=1m/s
EPmax2= (MA+MC)v′AC2+
(MA+MC)v′AC2+ MBvB2-
MBvB2- (MA+MB+MC)v共2=0.45J
(MA+MB+MC)v共2=0.45J
由上可得:橡皮绳具有的最大弹性势能的可能值在0.45J-1.35J的范围内.
答:(1)如图所示;(2)此后橡皮绳的最大弹性势能为1.25J;(3)橡皮绳具有的最大弹性势能的可能值在0.45J-1.35J的范围内.
点评:本题主要考查了动量守恒定律,能量守恒定律的应用,解题的关键是分析小球的运动情况,知道什么时候弹性势能最大,过程较为复杂,难度较大,属于难题.
(2)根据动量守恒定律求出AC共同速度,再求出碰撞损失的机械能,当三球速度相同时橡皮绳子弹性势能最大,根据能量关系求出橡皮绳的最大弹性势能;
(3)当A球在运动过程中速度为4m/s与C球同向时,C球与之相碰时系统损失能量最小(为0),橡皮绳具有的最大弹性势能,当A球在运动过程中速度为2m/s与C球反向时(此时B的速度为,C球与之相碰时系统损失能量最大,橡皮绳具有的最大弹性势能,根据能量关系求解此最大弹性势能,最后求出范围.
解答:
 解:(1)AB运动过程中动量守恒,根据动量守恒定律得:
解:(1)AB运动过程中动量守恒,根据动量守恒定律得:MAv=MAvA+MBvB
当vA=6m/s时vB=0
当vA=2m/s时vB=2m/s
当vA=-2m/s时vB=4m/s
所以一个周期内B球的v-t图象如图所示:
(2)AC碰撞,动量守恒:MAvA+MCvC=(MA+MC)vAC
解得:vAC=3m/s
碰撞损失的机械能为:△EK=
 MAvA2+
MAvA2+ MCvC2-
MCvC2- (MA+MC)vAC2=0.1J
(MA+MC)vAC2=0.1J当三球速度相同时橡皮绳子弹性势能最大,MAv+MCvC=(MA+MB+MC)v共
解得:v共=2.5m/s
所以 EPmax=
 MAv2+
MAv2+ MCvC2-
MCvC2- =(MA+MB+MC)v共2-△EK
=(MA+MB+MC)v共2-△EK解得:EPmax=1.25J
(3)①:当A球在运动过程中速度为4m/s与C球同向时,C球与之相碰时系统损失能量最小(为0),橡皮绳具有的最大弹性势能为EPmax1
EPmax1=
 MAv2+
MAv2+ MCvC2-
MCvC2- (MA+MB+MC)v共2=1.35J
(MA+MB+MC)v共2=1.35J②:当A球在运动过程中速度为2m/s与C球反向时(此时B的速度为,C球与之相碰时系统损失能量最大,橡皮绳具有的最大弹性势能为EPmax2,
MCvC-MAvA=(MA+MC)v′AC
解得v′AC=1m/s
EPmax2=
 (MA+MC)v′AC2+
(MA+MC)v′AC2+ MBvB2-
MBvB2- (MA+MB+MC)v共2=0.45J
(MA+MB+MC)v共2=0.45J由上可得:橡皮绳具有的最大弹性势能的可能值在0.45J-1.35J的范围内.
答:(1)如图所示;(2)此后橡皮绳的最大弹性势能为1.25J;(3)橡皮绳具有的最大弹性势能的可能值在0.45J-1.35J的范围内.
点评:本题主要考查了动量守恒定律,能量守恒定律的应用,解题的关键是分析小球的运动情况,知道什么时候弹性势能最大,过程较为复杂,难度较大,属于难题.

练习册系列答案
相关题目

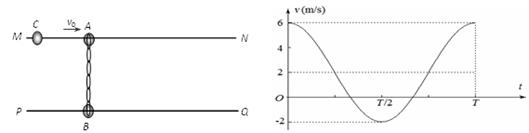
 ,以向右为速度正方向,以小球A获得速度开始计时得到A球的v-t图象如图(b)所示。(以后的运动中橡皮绳的伸长均不超过其弹性限度。)
,以向右为速度正方向,以小球A获得速度开始计时得到A球的v-t图象如图(b)所示。(以后的运动中橡皮绳的伸长均不超过其弹性限度。)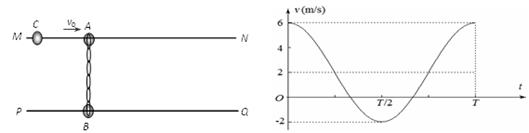
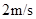 时,C遇到小球A,则此后橡皮绳的最大弹性势能为多少?
时,C遇到小球A,则此后橡皮绳的最大弹性势能为多少?