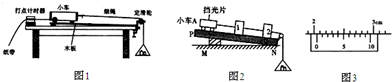
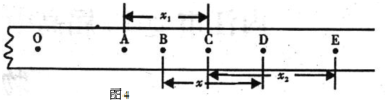
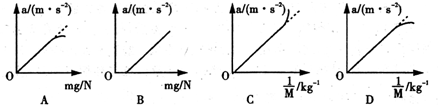
题目内容
如图所示，用与竖直方向成37°角的力F将重力为G=44N的物体推靠在竖直墙上，物体与竖直墙壁间动摩擦因数为μ=0.5，要使物体沿墙面匀速下滑，试求F的大小．（sin37°=0.6，cos37°=0.8）分析：对滑块受力分析，受重力、推力、支持力和滑动摩擦力；物体匀速下滑，合力为零；根据平衡条件列式求解．
解答：解：物体受力分析如图所示：
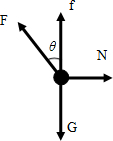
建立水平和竖直坐标系，把F正交分解，由平衡条件可得：
水平方向：N-Fsinθ=0
竖直方向：Fcosθ+f-G=0
又因为：f=μN
代入数据解得：F=
=
N=40N
答：推力F的大小为40N．
建立水平和竖直坐标系，把F正交分解，由平衡条件可得：
水平方向：N-Fsinθ=0
竖直方向：Fcosθ+f-G=0
又因为：f=μN
代入数据解得：F=
| mg |
| cosθ+μsinθ |
| 44 |
| 0.8+0.5×0.6 |
答：推力F的大小为40N．
点评：本题关键是对物体受力分析，运用平衡条件并结合正交分解法列式求解，不难．
练习册系列答案
相关题目
如图所示，在竖直方向上A、B两物体通过轻质弹簧相连，A放在水平地面上；B、C两物体通过细绳绕过轻质定滑轮相连，C放在固定的光滑斜面上．用手固定C，使细线刚刚拉直但无拉力作用，并保证ab段的细线竖直、cd段的细线与斜面平行．已知A、B的质量均为m，C的质量为4m．细线与滑轮之间的摩擦不计，开始时整个系统处于静止状态．释放C后它沿斜面下滑，A刚离开地面时B获得最大速度．则下列说法正确的是（ ）
如图所示，用轻绳吊一个重为G的小球，欲施一力F使小球在图示位置平衡（θ＜30°），下列说法正确的是（ ）| A、力F最小值为G?sinθ | B、若力F与绳拉力大小相等，力F方向与竖直方向必成θ角 | C、若力F与G大小相等，力F方向可以在竖直方向上 | D、若力F与G大小相等，力F方向与竖直方向可成2θ角 |
学过单摆的周期公式以后，物理兴趣小组的同学们对钟摆产生了兴趣，老师建议他们先研究用厚度和质量分布均匀的方木块(如一把米尺)做成的摆(这种摆被称为复摆)，如图所示.让其在竖直平面内做小角度摆动，C点为重心，板长为L，周期用T表示.
甲同学猜想：复摆的周期应该与板的质量有关.
乙同学猜想：复摆的摆长应该是悬点到重心的距离L／2.
丙同学猜想；复摆的摆长应该大于L／2.理由是：若OC段看成细线，线栓在C处，C点以下部分的重心离O点的距离显然大于L／2.
为了研究以上猜想是否正确，同学们进行了下面的实验探索：
(1)把两个相同的木板完全重叠在一起，用透明胶(质量不计)粘好，测量其摆动周期，发现与单个木板摆动时的周期相同，重做多次仍有这样的特点.则证明了甲同学的猜想是__________的(选填“正确”或“错误”).
(2)用T0表示板长为L的复摆看成摆长为L／2单摆的周期计算值(T0=2π
)，用T表示板长为L复摆的实际周期测量值.计算与测量的数据如下表：
板长L/cm | 25 | 50 | 80 | 100 | 120 | 150 |
周期计算值T0/s | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
周期测量值T/s | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
由上表可知，复摆的等效摆长___________L／2(选填“大于”“小于”或“等于”).
(3)为了进一步定量研究，同学们用描点作图法对数据进行处理，所选坐标如图.请在坐标纸上作出T—T0图，并根据图像中反映出的规律求出
=____________(结果保留三位有效数字，其中L等是板长为L时的等效摆长T=2π
).