题目内容
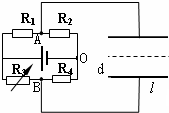 (2008?湖北模拟)如图所示,电源电动势为E=200V,内阻不计,R1、R2、R4的阻值均为300Ω,R3为可变电阻.C为一水平放置的平行板电容器,虚线到两极板距离相等,极板长为L=8cm,板间距离为d=1cm,.有一细电子束沿图中虚线以E0=1.92×103eV的动能连续不断地向右射入平行板电容器.已知电子电量e=1.6×10-19C,电子重力不计,求:
(2008?湖北模拟)如图所示,电源电动势为E=200V,内阻不计,R1、R2、R4的阻值均为300Ω,R3为可变电阻.C为一水平放置的平行板电容器,虚线到两极板距离相等,极板长为L=8cm,板间距离为d=1cm,.有一细电子束沿图中虚线以E0=1.92×103eV的动能连续不断地向右射入平行板电容器.已知电子电量e=1.6×10-19C,电子重力不计,求:(1)要使电子能沿直线飞出电容器,变阻器R3的取值多大?
(2)要使电子都能从电容器两极板间飞出,变阻器R3的取值范围多大?
分析:(1)根据匀速直线运动,可知AB两点的电压;从而由对称性,可确定求解;
(2)根据粒子做类平抛运动,结合飞出电场的偏转位移范围,再由牛顿第二定律与运动学公式,及闭合电路欧姆定律,即可求解.
(2)根据粒子做类平抛运动,结合飞出电场的偏转位移范围,再由牛顿第二定律与运动学公式,及闭合电路欧姆定律,即可求解.
解答:解:
(1)当电子匀速直线通过两极板时,两点电压UAB=0,设φ0=0
由对称性知,UAO=UBO时,有:
=
解得:R3=300Ω
(2)电子在电场中偏转的能飞出电场的临界条件为:y=
此时对应平行板电容器两极板间电压的最大值,有:y=
=
化简得:Um=
=60V
取O点为零势面,当UAB=Um=60V时
UAO=
R2=100V,
则?A=100V
?B=40V
UBO=
R4=40V
解得:R3=1200Ω
由题意可得,R3越小,B点电势越高,电子可以射出,因此为最大值
当UBA=Um=60V时,而A点电势不变,此时?B=160V
同理解得:R3=75Ω,此时R3越大,B点电势越低,电子可以射出;
综上所述:75Ω≤R3≤1200Ω
答:(1)要使电子能沿直线飞出电容器,变阻器R3的取值300Ω;
(2)要使电子都能从电容器两极板间飞出,变阻器R3的取值范围75Ω≤R3≤1200Ω.
(1)当电子匀速直线通过两极板时,两点电压UAB=0,设φ0=0
由对称性知,UAO=UBO时,有:
| ER2 |
| R1+R2 |
| ER4 |
| R3+R4 |
解得:R3=300Ω
(2)电子在电场中偏转的能飞出电场的临界条件为:y=
| d |
| 2 |
此时对应平行板电容器两极板间电压的最大值,有:y=
| d |
| 2 |
| eUml2 | ||
md
|
化简得:Um=
| 2E0d2 |
| el2 |
取O点为零势面,当UAB=Um=60V时
UAO=
| E |
| R1+R2 |
则?A=100V
?B=40V
UBO=
| E |
| R3+R4 |
解得:R3=1200Ω
由题意可得,R3越小,B点电势越高,电子可以射出,因此为最大值
当UBA=Um=60V时,而A点电势不变,此时?B=160V
同理解得:R3=75Ω,此时R3越大,B点电势越低,电子可以射出;
综上所述:75Ω≤R3≤1200Ω
答:(1)要使电子能沿直线飞出电容器,变阻器R3的取值300Ω;
(2)要使电子都能从电容器两极板间飞出,变阻器R3的取值范围75Ω≤R3≤1200Ω.
点评:考查粒子做匀速直线运动与类平抛运动,掌握牛顿第二定律与运动学公式的应用,理解运动的合成与分解的处理方法,并掌握闭合电路欧姆定律的运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 (2008?湖北模拟)如图所示,由电动机带动的水平传送带以速度为v=2.0m/s匀速运行,A端上方靠近传送带料斗中装有煤,打开阀门,煤以流量为Q=50kg/s落到传送带上,煤与传送带达共同速度后被运至B端,在运送煤的过程中,下列说法正确的是( )
(2008?湖北模拟)如图所示,由电动机带动的水平传送带以速度为v=2.0m/s匀速运行,A端上方靠近传送带料斗中装有煤,打开阀门,煤以流量为Q=50kg/s落到传送带上,煤与传送带达共同速度后被运至B端,在运送煤的过程中,下列说法正确的是( ) (2008?湖北模拟)如图所示,质量为m的小球用水平弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度为( )
(2008?湖北模拟)如图所示,质量为m的小球用水平弹簧系住,并用倾角为30°的光滑木板AB托住,小球恰好处于静止状态.当木板AB突然向下撤离的瞬间,小球的加速度为( ) (2008?湖北模拟)如图所示,平行直线表示电场线,但未标方向,带电量为10-2C的微粒在电场中只受电场力作用,由A点移到B点,动能损失0.1J,若A点电势为-10V,则( )
(2008?湖北模拟)如图所示,平行直线表示电场线,但未标方向,带电量为10-2C的微粒在电场中只受电场力作用,由A点移到B点,动能损失0.1J,若A点电势为-10V,则( ) (2008?湖北模拟)如图所示,地面上有两个完全相同的木块A、B,在水平推力F作用下运动,当弹簧长度稳定后,若用μ表示木块与地面间的动摩擦因数,FN表示弹簧弹力,则( )
(2008?湖北模拟)如图所示,地面上有两个完全相同的木块A、B,在水平推力F作用下运动,当弹簧长度稳定后,若用μ表示木块与地面间的动摩擦因数,FN表示弹簧弹力,则( )