Question

（2011?双流县模拟）如图1所示，建立Oxy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，第一、四象限有磁场，方向垂直于Oxy平面向里．位于极板左侧的粒子源沿x轴向右连续发射质量为m、电量为+q、速度相同、重力不计的带电粒子．在0～3t₀时间内两板间加上如图2所示的电压（不考虑极板边缘的影响）．已知t=0时刻进入两板间的带电粒子恰好在t₀时刻经极板边缘射入磁场．上述m、q、l、t₀、B为已知量．（不考虑粒子间相互影响及返回板间的情况）求：
（1）两板间的电压U₀．
（2）0～3t₀时间内射入两板间的带电粒子在磁场中运动的最短时间t．
（3）

1

2

t₀时刻射入两板间的带电粒子进入磁场和离开磁场时的位置坐标．

Answer 1

分析：（1）首先求出电容器加有电压时的电场强度，从而求出有电场时的加速度，把粒子的运动在竖直方向上分为两段，先是匀加速运动，后是匀速运动，在竖直方向上，这两段位移的和大小上等于板间距离的一半．列式即可求出电压．
（2）带电粒子在磁场中的运动时间最短，即为进入磁场时速度方向与y轴的夹角最小的情况，当在电场中偏转的角度最大时，在磁场中的运动时间最短，画出离子运动的轨迹图，结合几何知识即可求出最短时间．
（3），

1

2

t₀时刻进入两极板的带电粒子，前

1

2

t₀时间在电场中偏转，后

1

2

t₀时间两极板没有电场，带电粒子做匀速直线运动离开电场．根据运动学规律求出y方向分速度与x方向分速度，再合成求出粒子进入磁场时的速度，则牛顿定律求出粒子在磁场中做圆周运动的半径，进而求出离开磁场时的位置坐标．

解答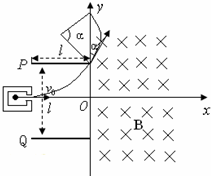：（1）t=0时刻进入两极板的带电粒子在电场中做类平抛运动，t₀时刻刚好从极板边缘射出，在y轴负方向偏移的距离为

1

2

l，则有：
E=

U0

l

…①
Eq=ma…  ②

1

2

l=

1

2

at02…③
联立解得两极板间偏转电压为：U0=

ml2

qt02

              
（2）2t₀时刻进入两极板的带电粒子在磁场中运动时间最短．
带电粒带电粒子离开磁场时沿y轴正方向的分速度为：v_y=at₀
设粒子离开电场时速度方向与y轴正方向的夹角为α，则：tanα=

v0

vy

解得：α=

π

4

所以圆心角为：2α=

π

2

由牛顿运动定律得：qbv=m

v2

R

周期：T=

2πR

v

联立求得最短时间为：t=

T

4

=

πm

2qB

（3）如上所述，

1

2

t₀时刻进入两极板的带电粒子，前

1

2

t₀时间在电场中偏转，后

1

2

t₀时间两极板没有电场，带电粒子做匀速直线运动离开电场．
由③式

1

2

a

t

2 0

=

1

2

l，则在前

1

2

t₀时间沿y轴方向的位移：

y

1

=

1

8

l
之后

1

2

t₀时间沿y轴方向的位移：

y

2

=2y1=

1

4

l
故带电粒子与y轴相交的坐标为：y=-(

y

2

+y1)=-

3

8

l，即带电粒子进入磁场时的位置坐标为：(0，-

3l

8

)设
带电粒子离开电场时速度方向与y轴负方向的夹角为β，则：tanβ=

v0

vy

=

l t0

1 2 at0

=2
此后受到洛伦兹力向上偏转，利用几何关系可以求得带电粒子进入磁场和离开磁场时的位置相距：△y=2Rsinβ=

4

5

R
又 带电粒子离开电场时沿y轴负方向的分速度大小为：vy=a?

1

2

t0
带电粒子离开电场时的速度大小为：v=

vx2+vy2

                 
设带电粒子离开电场进入磁场做匀速圆周运动的半径为R，则有：Bqv=m

v2

R

由以上各式解得：R=

5 ml

2qBt0

；                                     
 子沿x轴方向的分速度大小为：v0=

l

t0

          
故：△y=

4

5

R=

2ml

qBt0

，
因此带电粒子离开磁场时的位置在y轴的坐标：
Y=△y+y=

2ml

qBt0

-

3l

8

，
即带电粒子离开磁场时的位置坐标为：（0，

2ml

Bqt0

-

3l

8

）
答：（1）两板间的电压U₀为

ml2

qt02

．
（2）0～3t₀时间内射入两板间的带电粒子在磁场中运动的最短时间为

πm

2qB

．
（3）

1

2

t₀时刻射入两板间的带电粒子进入磁场和离开磁场时的位置坐标为（0，

2ml

Bqt0

-

3l

8

）．

点评：该题考查到的知识点较多，首先是考察到了离子在匀强电场中的偏转，并且电场还是变化的，这就要求我们要有较强的过程分析能力，对物体的运动进行分段处理；还考察到了离子在匀强磁场中的偏转，要熟练的会用半径公式和周期公式解决问题；在解决粒子在有界磁场中的运动时间问题时，要注意偏转角度与运动时间的关系，熟练的运用几何知识解决问题．是一道难度较大的题．