题目内容
（2007?深圳模拟）如图所示，在处于水平方向的细管内的端点O固定一根长为l、劲度系数为k的轻弹簧，在弹簧的自由端连接一个质量为m的小球，今将细管以O为轴逆时针缓慢转动，直至转到竖直方向，在此过程中，下列说法正确的是（ ）分析：将平板以O为转轴在竖直平面内逆时针缓慢转动，直至平板变为竖直状态，小球始终处于平衡状态，抓住小球重力沿斜面方向上的分力与弹簧弹力大小相等，得出形变量的变化，从而得出高度的关系式，通过关系式判断高度的变化，从而判断重力势能的变化．
解答：解：设转过的角度为θ，则mgsinθ=kx，则弹簧的形变量x=
．
球的高度h=（l-x）sinθ=（l-
）sinθ=-
(sinθ-
)2+
．因为sinθ＜1．
所以当弹簧的长度l一定，则球的质量m足够大时，
＜1，则h先增大后减小，所以小球的重力势能先增大后减小．
当球的质量m一定，则弹簧的长度l足够小时，
＜1，则h先增大后减小，所以小球的重力势能先增大后减小．故B正确，A、C、D错误．
故选B．
| mgsinθ |
| k |
球的高度h=（l-x）sinθ=（l-
| mgsinθ |
| k |
| mg |
| k |
| kl |
| 2mg |
| kl2 |
| 4mg |
所以当弹簧的长度l一定，则球的质量m足够大时，
| kl |
| 2mg |
当球的质量m一定，则弹簧的长度l足够小时，
| kl |
| 2mg |
故选B．
点评：本题对数学能力的要求较高，通过二次函数的方法并对sinθ的讨论得出高度的变化，从而判断重力势能的变化．
练习册系列答案
相关题目
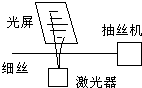（2007?深圳模拟）抽取高强度纤维细丝时可用激光监控其粗细，如图所示，观察激光束经过细丝时在光屏上所产生的条纹即可判断细丝粗细的变化．则（ ）
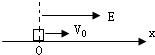（2007?深圳模拟）在一个水平面上建立x轴，在过原点O垂直于x轴的平面的右侧空间有一匀强电场，场强大小E=6×105N/C，方向与x轴正方向相同，在O处放一个带负电q=5×10-8C，质量为m=10g的绝缘物块（可看作质点），物块与水平面间的动摩擦因数μ=0.2，沿x轴正方向给物块一个初速度v0=2m/s，如图所示，求物块最终停止时的位置．
（2007?深圳模拟）直线CD是某电场中的一条电场线，若将一电子从A点处静止释放，电子沿电场线从A到B运动过程中的速度随时间变化的图线如图所示．则A、B两点的电势ФA、ФB的高低和场强EA、EB及电子在A、B两点的电势能εA、εB的大小关系是（ ）