题目内容
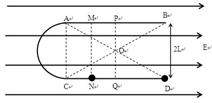
如图所示,一“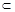 ”形绝缘导轨竖直放置,处在水平向右的匀强电场中。左边的半圆弧与水平杆AB、CD相切于A、C两点,两水平杆的高度差为2L,杆AB、CD长度均为4L,O为AD、BC连线的交点,虚线MN、PQ的位置如图,其中AM ="MP" =" CN" =" NQ="
L,PB=QD=2L。虚线MN左边的导轨光滑,虚线MN右边的导轨与小球之间的动摩擦因数为μ。现把一质量为m,电荷量为-q的小球穿在杆上,自N点由静止释放后,小球刚好可到达A点。已知静电力常量为k,重力加速度为g。求
”形绝缘导轨竖直放置,处在水平向右的匀强电场中。左边的半圆弧与水平杆AB、CD相切于A、C两点,两水平杆的高度差为2L,杆AB、CD长度均为4L,O为AD、BC连线的交点,虚线MN、PQ的位置如图,其中AM ="MP" =" CN" =" NQ="
L,PB=QD=2L。虚线MN左边的导轨光滑,虚线MN右边的导轨与小球之间的动摩擦因数为μ。现把一质量为m,电荷量为-q的小球穿在杆上,自N点由静止释放后,小球刚好可到达A点。已知静电力常量为k,重力加速度为g。求
:
(1) 匀强电场的电场强度E的大小;
(2)小球到达半圆弧中点时,该小球对半圆弧轨道的压力大小;
(3)若在O处固定一点电荷+Q,并将该带电小球自D点以某速度向左瞬间推出,结果小球可沿杆运动到B点。求从D到B点过程中小球所受摩擦力的最大值。
(1) E=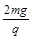 (2) N=8mg (3) fm=μ(mg +
(2) N=8mg (3) fm=μ(mg +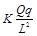 )
)
【解析】
试题分析:(1) 小球由N到A过程, 对小球列动能定理:
EqL—2mgL=0 (2分)
E=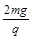 (2分)
(2分)
(2) 小球在圆弧的中点时,由牛顿第二定律得:
N—Eq=m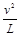 (2分)
(2分)
小球由N到圆弧的中点过程中,对小球列动能定理:
Eq(2L)—mgL=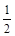 mv2
(2分)
mv2
(2分)
由 E=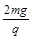 ,得
,得
N=8mg (2分)
由牛顿第三定律可知:N=N'=8mg (1分)
(3) 经分析可知,小球在P点的压力最大,则:
N=mg+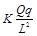 (1分)
(1分)
fm=μ N (1分)
fm=μ(mg +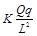 ) (1分)
) (1分)
考点:考查了动能定理以及牛顿第二定律的应用
点评:能够分析物体的受力情况和运动情况,选择合适的运动过程运用动能定理求解.动能定理的优点在于适用任何运动包括曲线运动.动能定理的应用范围很广,可以求速度、力、功等物理量,特别是可以去求变力功.

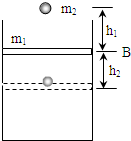 如图所示,内部横截面积为S的圆筒形绝热容器,封有一定质量的理想气体,开口向上放在硬板上.设活塞质量为m1,现有一质量为m2的橡皮泥从距活塞上表面高为h1处的A点由静止开始下落,碰到活塞后,随活塞一起下降的最大距离为h2,若不计活塞与容器壁的摩擦,求容器内气体内能的最大变化量是多少?
如图所示,内部横截面积为S的圆筒形绝热容器,封有一定质量的理想气体,开口向上放在硬板上.设活塞质量为m1,现有一质量为m2的橡皮泥从距活塞上表面高为h1处的A点由静止开始下落,碰到活塞后,随活塞一起下降的最大距离为h2,若不计活塞与容器壁的摩擦,求容器内气体内能的最大变化量是多少?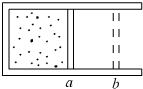 如图所示,有一固定的圆筒形绝热容器,用绝热活塞密封一定质量的气体,当活塞处于位置a时,筒内气体压强等于外界大气压,当活塞在外力作用下由位置a移动到位置b的过程中,下列说法正确的是( )
如图所示,有一固定的圆筒形绝热容器,用绝热活塞密封一定质量的气体,当活塞处于位置a时,筒内气体压强等于外界大气压,当活塞在外力作用下由位置a移动到位置b的过程中,下列说法正确的是( ) (2008?内江二模)如图所示.有一固定的圆筒形绝热容器,用绝热活塞密封了一定质量的气体(气体分子间相互作用的引力和斥力均忽略不计).当活塞处于位a时,筒内气体的压强等于外界的大气压强汽.当活塞在外力F的作用下由位置a移动到位置b的过程中,下列说法中正确的是( )
(2008?内江二模)如图所示.有一固定的圆筒形绝热容器,用绝热活塞密封了一定质量的气体(气体分子间相互作用的引力和斥力均忽略不计).当活塞处于位a时,筒内气体的压强等于外界的大气压强汽.当活塞在外力F的作用下由位置a移动到位置b的过程中,下列说法中正确的是( ) (2012?金山区一模)如图所示,固定的绝热气缸内有一质量为m的“T”型绝热活塞(体积可忽略),距气缸底部h0处连接一U形管(管内气体的体积忽略不计).初始时,封闭气体温度为T0,活塞距离气缸底部为1.5h0,两边水银柱存在高度差.已知水银的密度为ρ,大气压强为p0,气缸横截面积为s,活塞竖直部分长为1.2h0,重力加速度为g.试问:
(2012?金山区一模)如图所示,固定的绝热气缸内有一质量为m的“T”型绝热活塞(体积可忽略),距气缸底部h0处连接一U形管(管内气体的体积忽略不计).初始时,封闭气体温度为T0,活塞距离气缸底部为1.5h0,两边水银柱存在高度差.已知水银的密度为ρ,大气压强为p0,气缸横截面积为s,活塞竖直部分长为1.2h0,重力加速度为g.试问: (选修模块3-3)
(选修模块3-3)