题目内容
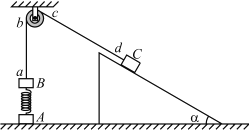
【题目】如图所示，A、B两物体之间用轻弹簧相连，B、C两物体用不可伸长的轻绳相连，并跨过轻质光滑定滑轮，C物体放置在固定的光滑斜面上.开始时用手固定C使绳处于拉直状态但无张力，ab绳竖直，cd绳与斜面平行.已知B的质量为m，C的质量为4m，弹簧的劲度系数为k，固定斜面倾角α=30°.由静止释放C，C在沿斜面下滑过程中A始终未离开地面.（已知弹簧的弹性势能的表达式为Ep=
kx2，x为弹簧的形变量.）重力加速度为g.求：
（1）刚释放C时，C的加速度大小；
（2）C从开始释放到速度最大的过程中，B上升的高度；
（3）若A不离开地面，其质量应满足什么条件。
【答案】（1）0.4g （2）
（3）
【解析】(1)刚释放C时，由牛顿第二定律；4mgsin300=5ma
解得：a=0.4g
(2)初始对B物体：kx1=mg
C速度最大时，F1=4mgsin300
此时，对B物体，F1=mg+kx2
B物体上升的高度h=x1+x2
解得：h=2mg/k
(3)若A不离开地面，则对A物体
kx1=mg
解得： 
练习册系列答案
相关题目
