题目内容
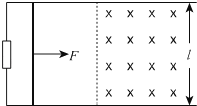
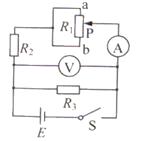
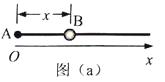
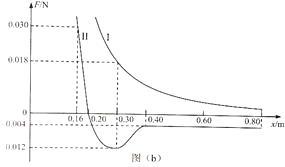
【题目】如图A.,长度L=0.8m的光滑杆左端固定一带正电的点电荷A,其电荷量Q= ![]() ;一质量m=0.02kg,带电量为q的小球B套在杆上。将杆沿水平方向固定于某非均匀外电场中,以杆左端为原点,沿杆向右为x轴正方向建立坐标系。点电荷A对小球B的作用力随B位置x的变化关系如图B.中曲线I所示,小球B所受水平方向的合力随B位置x的变化关系如图B.中曲线II所示,其中曲线II在0.16≤x≤0.20和x≥0.40范围可近似看作直线。求:(静电力常量
;一质量m=0.02kg,带电量为q的小球B套在杆上。将杆沿水平方向固定于某非均匀外电场中,以杆左端为原点,沿杆向右为x轴正方向建立坐标系。点电荷A对小球B的作用力随B位置x的变化关系如图B.中曲线I所示,小球B所受水平方向的合力随B位置x的变化关系如图B.中曲线II所示,其中曲线II在0.16≤x≤0.20和x≥0.40范围可近似看作直线。求:(静电力常量 ![]() )
)
①小球B所带电量q;
②非均匀外电场在x=0.3m处沿细杆方向的电场强度大小E;
③在合电场中,x=0.4m与x=0.6m之间的电势差U。
④已知小球在x=0.2m处获得v=0.4m/s的初速度时,最远可以运动到x=0.4m。若小球在x=0.16m处受到方向向右,大小为0.04N的恒力作用后,由静止开始运动,为使小球能离开细杆,恒力作用的做小距离s是多少?
【答案】①由图可知,当x=0.3m时, ![]() N
N
因此 ![]() C
C
②设在x=0.3m处点电荷与小球间作用力为F2 ,
F合=F2+qE
因此 ![]()
电场在x=0.3m处沿细秆方向的电场强度大小为3 ![]()
![]() ,方向水平向左。
,方向水平向左。
③根据图像可知在x=0.4m与x=0.6m之间合力做功大小
W合=0.004 ![]() 0.2=8
0.2=8 ![]() 10-4J
10-4J
由qU=W合
可得 ![]()
④由图可知小球从x=0.16m到x=0.2m处
电场力做功 ![]() J
J
小球从 ![]() 到
到 ![]() 处
处
电场力做功 ![]() =
= ![]()
![]() =
= ![]()
![]()
由图可知小球从 ![]() 到
到 ![]() 处
处
电场力做功 ![]() =-0.004×0.4=
=-0.004×0.4= ![]()
![]()
由动能定理 ![]() +
+ ![]() +
+ ![]() +
+ ![]() =0
=0
解得 ![]() =
= ![]()
【解析】①根据库仑定律可求小球B所带电量;②(2)根据电场强度的定义可求非均匀外电场在x=0.3m处沿细杆方向的电场强度大小;③在合电场中,根据电场力做功求x=0.4m与x=0.6m之间的电势差;④分别求出各段电场力做的功,再由动能定理求恒力作用的最小距离.
【考点精析】通过灵活运用动能定理的理解和库仑定律,掌握动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的.但它也适用于变力及物体作曲线运动的情况;功和动能都是标量,不能利用矢量法则分解,故动能定理无分量式;在真空中两个点电荷间的作用力跟它们的电荷量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在它们的连线上;适用条件:真空中的点电荷即可以解答此题.