题目内容
15.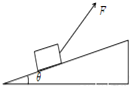 一个搬运工人通常最多能提起质量m0=25kg的重物.在倾角θ=30°的固定斜面上放置一物体(可视为质点),物体与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{3}$.设最大静摩擦力等于滑动摩擦力,求人能够向上拖动货物质量的最大值M.
一个搬运工人通常最多能提起质量m0=25kg的重物.在倾角θ=30°的固定斜面上放置一物体(可视为质点),物体与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{3}$.设最大静摩擦力等于滑动摩擦力,求人能够向上拖动货物质量的最大值M.
分析 对斜面上的物体进行受力分析,并将物体受到的力沿斜面方向与垂直于斜面的方向分解,求出M的表达式,然后结合三角函数的关系,即可求出最大质量.
解答 解:设F与斜面倾角为α时,拖动的重物最大质量为M,
由平衡条件可得:
Fcosα-Mgsin30°-μFN=0…①
FN+Fsinα-Mgcos30°=0…②
由已知可得:F=m0g…③
代入数据联立得:M=28.87kg…④
答:人能够向上拖动货物质量的最大值M为28.87kg.
点评 该题中按照常规的步骤对物体进行受力分析即可,题目的难点是如何利用三角函数的关系,化简并得出正确的结论.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.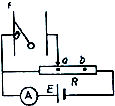 竖直放置的一对平行金属板的左极板上用绝缘线悬挂了一个带正电的小球,将平行金属板如图所示的电路图连接.绝缘线与左极板的夹角为θ,当滑动变阻器R的滑片在a位置时,电流表的读数为I1,夹角为θ1;当滑片在b位置时,电流表的读数为I2,夹角为θ2,则下列判断正确的是( )
竖直放置的一对平行金属板的左极板上用绝缘线悬挂了一个带正电的小球,将平行金属板如图所示的电路图连接.绝缘线与左极板的夹角为θ,当滑动变阻器R的滑片在a位置时,电流表的读数为I1,夹角为θ1;当滑片在b位置时,电流表的读数为I2,夹角为θ2,则下列判断正确的是( )
 竖直放置的一对平行金属板的左极板上用绝缘线悬挂了一个带正电的小球,将平行金属板如图所示的电路图连接.绝缘线与左极板的夹角为θ,当滑动变阻器R的滑片在a位置时,电流表的读数为I1,夹角为θ1;当滑片在b位置时,电流表的读数为I2,夹角为θ2,则下列判断正确的是( )
竖直放置的一对平行金属板的左极板上用绝缘线悬挂了一个带正电的小球,将平行金属板如图所示的电路图连接.绝缘线与左极板的夹角为θ,当滑动变阻器R的滑片在a位置时,电流表的读数为I1,夹角为θ1;当滑片在b位置时,电流表的读数为I2,夹角为θ2,则下列判断正确的是( )| A. | θ1<θ2,I1<I2 | B. | θ1>θ2,I1>I2 | C. | θ1=θ2,I1>I2 | D. | θ1<θ2,I1=I2 |
3.关于质点,下列说法中正确的是( )
| A. | 体积和质量极小的物体一定可以看作质点 | |
| B. | 研究汽车车轮上一个点的运动规律时,汽车可看作质点 | |
| C. | 欣赏花样滑冰表演者的精彩表演时,可以把表演者看作质点 | |
| D. | 研究运动员在1500米长跑比赛中一定的快慢时,该运动员可看作质点 |
10. 如图所示,在水平力F作用下,木块A、B保持静止.若木块A与B的接触面是水平的,且F≠0.则木块B的受力个数可能是( )
如图所示,在水平力F作用下,木块A、B保持静止.若木块A与B的接触面是水平的,且F≠0.则木块B的受力个数可能是( )
 如图所示,在水平力F作用下,木块A、B保持静止.若木块A与B的接触面是水平的,且F≠0.则木块B的受力个数可能是( )
如图所示,在水平力F作用下,木块A、B保持静止.若木块A与B的接触面是水平的,且F≠0.则木块B的受力个数可能是( )| A. | 3个 | B. | 7个 | C. | 5个 | D. | 6个 |
7.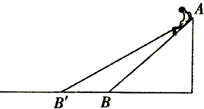 如图所示,某滑草场有两个坡度不同的滑道AB和AB′(均可看作斜面).质量相同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB和AB′滑下,最后都停在水平草面上,斜草面和水平草面平滑连接,滑草板与草面之间的动摩擦因数处处相同,下列说法正确的是( )
如图所示,某滑草场有两个坡度不同的滑道AB和AB′(均可看作斜面).质量相同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB和AB′滑下,最后都停在水平草面上,斜草面和水平草面平滑连接,滑草板与草面之间的动摩擦因数处处相同,下列说法正确的是( )
 如图所示,某滑草场有两个坡度不同的滑道AB和AB′(均可看作斜面).质量相同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB和AB′滑下,最后都停在水平草面上,斜草面和水平草面平滑连接,滑草板与草面之间的动摩擦因数处处相同,下列说法正确的是( )
如图所示,某滑草场有两个坡度不同的滑道AB和AB′(均可看作斜面).质量相同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB和AB′滑下,最后都停在水平草面上,斜草面和水平草面平滑连接,滑草板与草面之间的动摩擦因数处处相同,下列说法正确的是( )| A. | 甲沿斜草面下滑过程中克服摩擦力做的功比乙的多 | |
| B. | 甲乙经过斜草面底端的速率相等 | |
| C. | 甲、乙最终停在水平草面上的同一位置 | |
| D. | 甲停下时的位置与B的距离和乙停下时的位置与B′的距离相等 |
5. 一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
 一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )
一皮带传动装置,轮A、B均沿同方向转动,设皮带不打滑,a、b为两轮边缘上的点,某时刻a、b、o、o′位于同一水平面上,如图所示.设该时刻a、b所受摩擦力分别为fa、fb,则下列说法正确的是( )| A. | fa、fb都是动力、而且方向相同 | |
| B. | fa、fb都是阻力,而且方向相反 | |
| C. | fa若是动力,则fb一定是阻力,两力方向相反 | |
| D. | fa若是阻力,则fb一定是动力,两方向相同 |
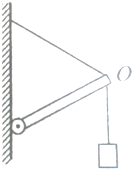 如图所示,轻杆与竖直墙壁之间用铰链连接,杆的末端吊着一个重为G的物体,墙与轻绳、杆之间的夹角都是θ=60°,求轻绳和杆各受多大的力?
如图所示,轻杆与竖直墙壁之间用铰链连接,杆的末端吊着一个重为G的物体,墙与轻绳、杆之间的夹角都是θ=60°,求轻绳和杆各受多大的力?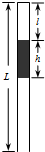 如图,一上端封闭、下端开口、总长L=100cm的玻璃管竖直放置.玻璃管的上部封有长l=25cm的空气柱,中间有一段长为h=25cm的水银柱.已知大气压为p0=75cmHg.现将一活塞(图中未画出)从玻璃管开口处缓慢往上推,使管内上部分空气柱长度变为l′=20cm,温度始终保持不变.求:
如图,一上端封闭、下端开口、总长L=100cm的玻璃管竖直放置.玻璃管的上部封有长l=25cm的空气柱,中间有一段长为h=25cm的水银柱.已知大气压为p0=75cmHg.现将一活塞(图中未画出)从玻璃管开口处缓慢往上推,使管内上部分空气柱长度变为l′=20cm,温度始终保持不变.求: