题目内容
20.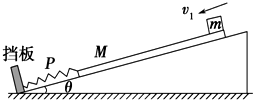 如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触、但不拴接,弹簧与斜面平行、且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到木块达到共速共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sin θ=0.28、cos θ=0.96,g取10m/s2,结果保留二位有效数字.
如图所示,斜面倾角为θ,在斜面底端垂直斜面固定一挡板,轻质弹簧一端固定在挡板上,质量为M=1.0kg的木板与轻弹簧接触、但不拴接,弹簧与斜面平行、且为原长,在木板右上端放一质量为m=2.0kg的小金属块,金属块与木板间的动摩擦因数为μ1=0.75,木板与斜面粗糙部分间的动摩擦因数为μ2=0.25,系统处于静止状态.小金属块突然获得一个大小为v1=5.3m/s、平行斜面向下的速度,沿木板向下运动.当弹簧被压缩x=0.5m到P点时,金属块与木板刚好达到相对静止,且此后运动过程中,两者一直没有发生相对运动.设金属块从开始运动到木块达到共速共用时间t=0.75s,之后木板压缩弹簧至最短,然后木板向上运动,弹簧弹开木板,弹簧始终处于弹性限度内,已知sin θ=0.28、cos θ=0.96,g取10m/s2,结果保留二位有效数字.(1)求木板开始运动瞬间的加速度;
(2)金属块和木板达到共同速度时弹簧的弹性势能;
(3)假设木板由P点压缩弹簧到弹回P点过程中不受斜面摩擦力作用,求木板离开弹簧后沿斜面向上滑行的距离.
分析 (1)运用隔离法分别对金属块和长木板进行受力分析,根据牛顿第二定律求加速度;
(2)根据动能定理求得弹簧压缩过程中做的功,再根据弹力做功与弹性势能变化的关系求得弹簧的弹性势能;
(3)根据能量转化和守恒定律求得木板离开弹簧后的速度,再根据动能定理求得木板上滑的最大距离
解答 解:(1)对金属块,由牛顿第二定律可知加速度大小为
a=μ1gcosθ-gsinθ=4.4 m/s2,沿斜面向上
木板受到金属块的滑动摩擦力F1=μ1mgcosθ=14.4 N,沿斜面向下
木板受到斜面的滑动摩擦力
F2=μ2(M+m)gcosθ=7.2 N,沿斜面向上
木板开始运动瞬间的加速度a0=$\frac{Mgsinθ+{F}_{1}-{F}_{2}}{M}$
解得a0=10 m/s2,沿斜面向下
(2)设金属块和木板达到共同速度为v2,对金属块,应用速度公式有
v2=v1-at=2.0 m/s
在此过程中以木板为研究对象,设弹簧对木板做功为W,对木板运用动能定理得
Ma0x+W=$\frac{1}{2}$Mv${\;}_{2}^{2}$
解得W=-3.0 J,
说明此时弹簧的弹性势能Ep=3.0 J
(3)金属块和木板达到共速后压缩弹簧,速度减小为0后反向弹回,设弹簧恢复原长时木板和金属块的速度为v3,在此过程中对木板和金属块,由能量的转化和守恒得:
Ep-(F2+Mgsinθ+mgsinθ)x=$\frac{1}{2}$(M+m)v${\;}_{3}^{2}$-$\frac{1}{2}$(M+m)v${\;}_{2}^{2}$
木板离开弹簧后,设滑行距离为s,由动能定理得:
-(M+m)g(μ2cosθ+sinθ)s=-$\frac{1}{2}$(M+m)v${\;}_{3}^{2}$
解得s=0.077 m
答:(1)木板开始运动瞬间的加速度为10m/s2方向沿斜面向下;
(2)弹簧被压缩到P点时的弹性势能是3.0J;
(3)假设木板在由P点压缩弹簧到弹回到P点过程中不受斜面摩擦力作用,木板离开弹簧后沿斜面向上滑行的距离为0.077m
点评 在应用牛顿运动定律和运动学公式解决问题时,要注意运动过程的分析,此类问题,还要对整个运动进行分段处理

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案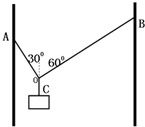 三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB与竖直方向的夹角为60°0A与竖直方向的夹角为30°,若逐渐增加C端所挂物体的质量,则最先断的绳( )
三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,如图所示,其中OB与竖直方向的夹角为60°0A与竖直方向的夹角为30°,若逐渐增加C端所挂物体的质量,则最先断的绳( )| A. | 必定是OA | B. | 必定是OB | ||
| C. | 必定是OC | D. | 可能是OB,也可能是OC |
| A. | 静止或做匀速直线运动的物体一定不受外力的作用 | |
| B. | 物体的速度为零时一定处于平衡状态 | |
| C. | 物体的运动状态发生变化时,一定受到外力的作用 | |
| D. | 物体的位移方向一定与所受合力方向一致 |
| A. | 伽利略通过理想斜面实验提出了惯性的概念 | |
| B. | 弹力的方向总是与引起形变的作用力的方向相同 | |
| C. | 国际单位制中,kg、m、N是三个基本单位 | |
| D. | 用国际单位制中的基本单位表示,电压的单位可写作kg•m2/(A.S3) |
 伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法中错误的是( )
伽利略为了研究自由落体的规律,将落体实验转化为著名的“斜面实验”,对于这个研究过程,下列说法中错误的是( )| A. | 斜面实验“冲淡”了重力的作用,便于小球运动时间的测量 | |
| B. | 经过合理外推,得到自由落体的运动与物体的质量无关 | |
| C. | 结论之一:倾角一定时,小球在斜面上的速度与时间成正比 | |
| D. | 研究方法:发现问题-实验验证-提出假设-逻辑推理-合理外推-得出结论 |

| A. | t2时刻,小物块离A处的距离达到最大 | |
| B. | t2时刻,小物块相对传送带滑动的距离达到最大 | |
| C. | 0~t2时间内,小物块受到的摩擦力方向始终向右 | |
| D. | 0~t3时间内,小物块受到的摩擦力大小始终不变 |
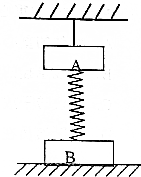 如图所示,A、B两物体由弹簧连接,A、B两物体的重力分别为G1=5N和G2=6N,不计弹簧质量,整个装置处于静止状态.这时弹簧的弹力F=3N.
如图所示,A、B两物体由弹簧连接,A、B两物体的重力分别为G1=5N和G2=6N,不计弹簧质量,整个装置处于静止状态.这时弹簧的弹力F=3N. 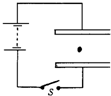 如图所示,水平放置的平行板电容器,电容为C,极板间的距离为d,板长为L,与电池组相连.当电键S闭合时,电容器中央一个质量为m、电量为q的油滴恰好处于静止状态.
如图所示,水平放置的平行板电容器,电容为C,极板间的距离为d,板长为L,与电池组相连.当电键S闭合时,电容器中央一个质量为m、电量为q的油滴恰好处于静止状态.