题目内容
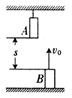
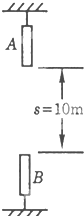 如图所示,A、B两棒均长l m,A悬于高处,B竖于地面.A的下端和B的上端相距s=10m.若A、B两棒同时运动,A做自由落体运动,B以初速度v0=20m/s做竖直上抛运动,在运动过程中都保持竖直.问:
如图所示,A、B两棒均长l m,A悬于高处,B竖于地面.A的下端和B的上端相距s=10m.若A、B两棒同时运动,A做自由落体运动,B以初速度v0=20m/s做竖直上抛运动,在运动过程中都保持竖直.问:(1)两棒何时开始相遇?
(2)擦肩而过(不相碰)的时间?(取g=10m/s2).
分析:两者相遇时位移之和等于s,两者从相遇开始到分离,经过的位移大小之和为2L.若以A为参考系,B以v0向上匀速运动,根据匀速直线运动的位移时间公式求出时间.
解答:解:(1)以A为参考系,B以v0向上匀速运动,在相遇的过程中,B的位移为s,根据匀速直线运动的公式得:
t=
=0.5s
(2)从相遇开始到分离所需时间,以A为参考系,B的位移为2L,根据匀速直线运动的公式得,
△t=
=0.05s.
答:(1)A、B经过0.5s相遇.
(2)擦肩而过(不相碰)的时间为0.05s.
t=
| S |
| v0 |
(2)从相遇开始到分离所需时间,以A为参考系,B的位移为2L,根据匀速直线运动的公式得,
△t=
| 2l |
| v0 |
答:(1)A、B经过0.5s相遇.
(2)擦肩而过(不相碰)的时间为0.05s.
点评:解决本题的巧妙之处是以A为参考系,B以v0向上匀速运动,根据匀速直线运动的公式进行求解.本题也可以地面为参考系,根据匀变速直线运动的公式求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
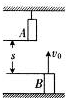 如图所示,A、B两棒长均为L=1m,A的下端和B的上端相距s=20m.若A、B同时运动,A做自由落体运动,B做竖直上抛运动,初速度v0=40m/s.求:(g=10m/s2)
如图所示,A、B两棒长均为L=1m,A的下端和B的上端相距s=20m.若A、B同时运动,A做自由落体运动,B做竖直上抛运动,初速度v0=40m/s.求:(g=10m/s2)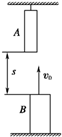 如图所示,A、B两棒长均为L=1m,A的下端和B的上端相距s=20m,若同时A做自由落体运动,B做初速度为v0=40m/s的竖直上抛运动,求:
如图所示,A、B两棒长均为L=1m,A的下端和B的上端相距s=20m,若同时A做自由落体运动,B做初速度为v0=40m/s的竖直上抛运动,求: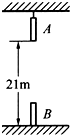 (2013?普陀区二模)如图所示,A、B两棒各长1m,A吊于高处,B竖直置于地面上,A的下端距地面21m.现让两棒同时开始运动,A自由下落,B以20m、s的初速度竖直上抛,若不计空气阻力,则两棒从一端相遇到另一端分离所经过的时间t为( )
(2013?普陀区二模)如图所示,A、B两棒各长1m,A吊于高处,B竖直置于地面上,A的下端距地面21m.现让两棒同时开始运动,A自由下落,B以20m、s的初速度竖直上抛,若不计空气阻力,则两棒从一端相遇到另一端分离所经过的时间t为( )