题目内容
表中记录了与地球、月球有关的数据资料(以地球为参考系),利用这些数据来计算地球表面与月球表面之间的距离s,下列方法正确的是( )
| ||||||||||||||||
分析:根据激光器发出激光束从发出到接收的时间和光速,可求出地球表面与月球表面之间的距离s.根据月球绕地球转动的线速度,求出月地间的距离,再求出s.月球绕地球做匀速圆周运动,由地球的万有引力提供向心力,由牛顿第二定律求出月地间的距离,再求出s.
解答:解:
A、由题,激光器发出激光束从发出到接收的时间为t=2.565s,光速为c,则s=c?
.故A正确.
B、月球表面的重力加速度g′与月球绕地球转动的线速度v没有关系,不能得到m月g0=
,故B错误.
C、月球绕地球转动的线速度为v=1km/s,周期为T=27.3s,轨道半径为R′=s+R+r,由v=
得,
s=
-R-r.故C正确.
D、以月球为研究对象,月球绕地球公转时,由地球的万有引力提供向心力,而万有引力近似等于月球的重力,则有
m月g″=m月
(s+R+r)
g″应是月球轨道处的重力加速度,不是月球表面的重力加速度g′,故D错误.
故选AC
A、由题,激光器发出激光束从发出到接收的时间为t=2.565s,光速为c,则s=c?
| t |
| 2 |
B、月球表面的重力加速度g′与月球绕地球转动的线速度v没有关系,不能得到m月g0=
| m月v2 |
| s+R+r |
C、月球绕地球转动的线速度为v=1km/s,周期为T=27.3s,轨道半径为R′=s+R+r,由v=
| 2π(s+R+r) |
| T |
s=
| vT |
| 2π |
D、以月球为研究对象,月球绕地球公转时,由地球的万有引力提供向心力,而万有引力近似等于月球的重力,则有
m月g″=m月
| 4π2 |
| T2 |
g″应是月球轨道处的重力加速度,不是月球表面的重力加速度g′,故D错误.
故选AC
点评:本题要理清思路,明确好研究的对象和过程,要充分利用表格的数据求解s,考查运用万有引力和圆周运动规律解决天体问题的能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2013年12月15日,“玉兔”登月车着月后牵动了亿万中华儿女的心.12月26日,玉兔进入为期14个地球日的月夜休眠期.某同学在学习中记录了一些与地球月球有关的数据资料如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中不正确的是( )
| ||||||||||||||||
2013年12月15日,“玉兔”登月车着月后牵动了亿万中华儿女的心。12月26日,玉兔进入为期14个地球日的月夜休眠期。某同学在学习中记录了一些与地球月球有关的数据资料如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中不正确的是( )
|
地球半径 |
R=6 400 km |
|
月球半径 |
r=1740 km |
|
地球表面重力加速度 |
g0=9.80m/s2 |
|
月球表面重力加速度 |
g′=1.56m/s2 |
|
月球绕地球转动的线速度 |
v=1 km/s |
|
月球绕地球转动的周期 |
T=27.3天 |
|
光速 |
c=2.998×108km/s |
|
用激光器向月球表面发射激光光束,经过约t=2.565 s接收到从月球表面反射回来的激光信号 |
A. B.
B. C.
C. D.
D.
表中记录了与地球、月球有关的数据资料(以地球为参考系),利用这些数据来计算地球表面与月球表面之间的距离s,下列方法正确的是( )
A.利用激光束的反射 来算
来算
B.利用地球表面的重力加速度、月球绕地球转动的线速度关系m月g= 来算
来算
C.利用月球绕地球转动的线速度、周期关系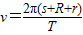 来算
来算
D.利用月球表面的重力加速度、月球绕地球转动的周期关系 来算
来算
| 地球半径 | R=6400km |
| 月球半径 | r=1740km |
| 地球表现重力加速度 | g=9.80m/s2 |
| 月球表面重力加速度 | g′=1.56m/s2 |
| 月球绕地球转动的线速度 | v=1km/s |
| 月球绕地球转动周期 | T=27.3天 |
| 光速 | c=2.998×105km/s |
| 用激光器向月球表面发射激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号 | |
A.利用激光束的反射
 来算
来算B.利用地球表面的重力加速度、月球绕地球转动的线速度关系m月g=
 来算
来算C.利用月球绕地球转动的线速度、周期关系
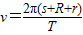 来算
来算D.利用月球表面的重力加速度、月球绕地球转动的周期关系
 来算
来算(2013年3月吉林二模)某同学在学习中记录了一些与 地球、月球有关的数据资料如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则下列运算公式中正确的是
A. c ![]()
B.![]() -R-r
-R-r
C.![]() -R-r
-R-r
D.![]() -R-r
-R-r
用激光器向月球表面发射激光光束,经过约t=2.565s接收到从月球表面反射回来的激光信号 |