题目内容
17. 如图所示,MN表示真空室中垂直于纸面放置的感光板,它的上侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B,一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域,最后到达感光板上的P点.经测量P、O间的距离为l,不计带电粒子受到的重力.求:
如图所示,MN表示真空室中垂直于纸面放置的感光板,它的上侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度大小为B,一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域,最后到达感光板上的P点.经测量P、O间的距离为l,不计带电粒子受到的重力.求:(1)带电粒子在磁场中做匀速圆周运动的半径大小
(2)带电粒子的质量大小
(3)带电粒子在磁场中的运动时间.
分析 (1)根据图示粒子运动轨迹,由几何知识可以求出粒子的轨道半径.
(2)粒子做圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出粒子的质量.
(3)根据粒子在磁场中转过的圆心角与粒子做圆周运动的周期可以求出粒子的运动时间.
解答 解:(1)根据图示粒子运动轨迹,由几何知识可知,粒子轨道半径:r=$\frac{1}{2}$l;
(2)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:m=$\frac{qBl}{2v}$;
(3)由图示可知,粒子在磁场中转过半个圆周,
粒子在磁场中的运动时间:t=$\frac{1}{2}$T=$\frac{1}{2}$×$\frac{2πr}{v}$=$\frac{πl}{2v}$;
答:(1)带电粒子在磁场中做匀速圆周运动的半径大小为$\frac{1}{2}$l;
(2)带电粒子的质量大小为$\frac{qBl}{2v}$;
(3)带电粒子在磁场中的运动时间为$\frac{πl}{2v}$.
点评 带电粒子在匀强磁场中做圆周运动,由洛伦兹力提供向心力,根据题意作出粒子的运动轨迹,由几何知识求解半径,再由牛顿定律和圆周运动的规律结合研究.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
8. 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点,现在提起自行车后轮、转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点,现在提起自行车后轮、转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
 如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点,现在提起自行车后轮、转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )
如图为某品牌自行车的部分结构.A、B、C分别是飞轮边缘、大齿盘边缘和链条上一个点,现在提起自行车后轮、转动脚蹬子,使大齿盘和飞轮在链条带动下转动,则下列说法正确的是( )| A. | A、B、C三点线速度大小不相等 | |
| B. | A、B两点的角速度大小相等 | |
| C. | 由图中信息,A、B两点的角速度之比为3:1 | |
| D. | A、B两点的向心加速度与飞轮、大齿盘半径成反比 |
5. 如图所示,MN是一匀强电场中的一条电场线,一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
如图所示,MN是一匀强电场中的一条电场线,一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
 如图所示,MN是一匀强电场中的一条电场线,一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )
如图所示,MN是一匀强电场中的一条电场线,一个带正电的粒子(不计重力)从a到b穿越这条电场线的轨迹如图中虚线所示.下列结论正确的是( )| A. | 电场线的方向由M指向N | |
| B. | a点的电势高于b点电势 | |
| C. | 粒子在a点的电势能大于在b点的电势能 | |
| D. | 粒子从a到b过程中机械能不变 |
2.某个行星的质量是地球质量的一半,半径也是地球半径的一半,那么一个物体在此行星表面上受到的重力是其在地球表面上受到的重力的( )
| A. | $\frac{1}{4}$倍 | B. | 2倍 | C. | 4倍 | D. | $\frac{1}{2}$倍 |
6.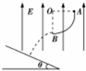 如图,一质量为m、带电荷量为+q的小球从半径为R的四分之一绝缘光滑圆弧轨道上与圆心等高处A由静止释放,经时间t下滑到轨道最低点B时对轨道压力为2mg,g为重力加速度,此后小球水平飞出,恰好垂直击中倾角为θ=30°的斜面,整个斜面上方存在竖直向上的匀强电场,空气阻力不计,则下列说法中正确的是( )
如图,一质量为m、带电荷量为+q的小球从半径为R的四分之一绝缘光滑圆弧轨道上与圆心等高处A由静止释放,经时间t下滑到轨道最低点B时对轨道压力为2mg,g为重力加速度,此后小球水平飞出,恰好垂直击中倾角为θ=30°的斜面,整个斜面上方存在竖直向上的匀强电场,空气阻力不计,则下列说法中正确的是( )
 如图,一质量为m、带电荷量为+q的小球从半径为R的四分之一绝缘光滑圆弧轨道上与圆心等高处A由静止释放,经时间t下滑到轨道最低点B时对轨道压力为2mg,g为重力加速度,此后小球水平飞出,恰好垂直击中倾角为θ=30°的斜面,整个斜面上方存在竖直向上的匀强电场,空气阻力不计,则下列说法中正确的是( )
如图,一质量为m、带电荷量为+q的小球从半径为R的四分之一绝缘光滑圆弧轨道上与圆心等高处A由静止释放,经时间t下滑到轨道最低点B时对轨道压力为2mg,g为重力加速度,此后小球水平飞出,恰好垂直击中倾角为θ=30°的斜面,整个斜面上方存在竖直向上的匀强电场,空气阻力不计,则下列说法中正确的是( )| A. | 小球从A到B的平均速度为$\frac{πR}{2t}$ | |
| B. | 匀强电场的电场强度大小为$\frac{mg}{3q}$ | |
| C. | 小球从开始运动到击中斜面的过程中机械能守恒 | |
| D. | 小球从圆弧轨道飞出到击中斜面的时间为3$\sqrt{\frac{R}{g}}$ |
7.如图所示电路中,C2=2C1,R2=2R1,下列说法正确的是( )
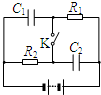

| A. | 开关处于断开状态,电容C1的电量大于电容C2的电量 | |
| B. | 开关处于断开状态,电容C2的电量大于电容C1的电量 | |
| C. | 开关处于接通状态,电容C2的电量大于电容C1的电量 | |
| D. | 开关处于接通状态,电容C1的电量等于电容C2的电量 |

 在验证机械能守恒的实验中选出一条纸带,如图所示,O为打点计时器打出的第一个点,A、B、C是三个记数点,打点计时器接50Hz的交流电,用最小刻度为mm的刻度测得OA=11.13cm,OB=11.75cm,OC=25.9cm,这三个数据中不符合有效数字要求的是OC,应该写成25.90.在A和B之间,B和C之间还各有一个点,重锤的质量为mkg,根据以上数据,当打点针打至点B时重锤的重力势能比开始下落时减少了1.74mJ;这时它的动能是1.71mJ(g取9.80m/s2)
在验证机械能守恒的实验中选出一条纸带,如图所示,O为打点计时器打出的第一个点,A、B、C是三个记数点,打点计时器接50Hz的交流电,用最小刻度为mm的刻度测得OA=11.13cm,OB=11.75cm,OC=25.9cm,这三个数据中不符合有效数字要求的是OC,应该写成25.90.在A和B之间,B和C之间还各有一个点,重锤的质量为mkg,根据以上数据,当打点针打至点B时重锤的重力势能比开始下落时减少了1.74mJ;这时它的动能是1.71mJ(g取9.80m/s2)