题目内容
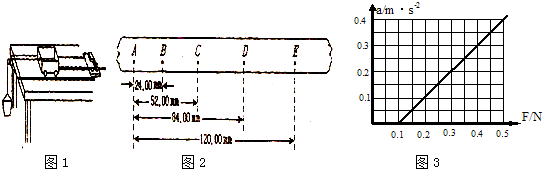
用如图1所示实验装置验证机械能守恒定律.水平桌面上固定一倾斜的气垫导轨,导轨上A点处有一带长方形遮光片的滑块,其总质量为m,遮光片两条竖边与导轨垂直;导轨上B点处有一光电门,测得遮光片经过光电门时的挡光时间为t,用d表示A点到导轨底端C点的距离,h表示A与C的高度差,b表示遮光片的宽度,s表示A、B两点间的距离.将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度,用g表示重力加速度.完成下列填空和作图:
(1)若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片组成的系统重力势能的减小量表示为△EP=
.动能的增加量表示为△Ek=
.在滑块运动过程中若机械能守恒,则与s的关系式为=
=
=
.
(2)多次改变光电门的位置,每次均令滑块自同一点(A点)下滑,测量相应的s与t值,结果如下表所示:
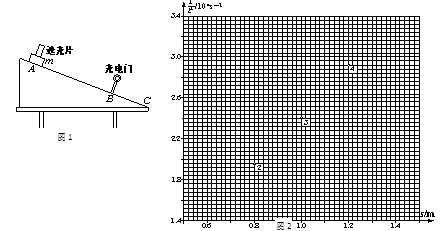
以s为横坐标,为纵坐标,在如图2的坐标纸中已经描出2、3、4数据点;请描出第1和第5个数据点,并根据5个数据点作直线,求得该直线的斜率:k=
,计算出k0的值,然后将k和k0进行比较,若其差值在实验误差允许的范围内,则可认为此实验验证了机械能守恒定律.

(1)若将滑块自A点由静止释放,则在滑块从A运动至B的过程中,滑块、遮光片组成的系统重力势能的减小量表示为△EP=
| mghs |
| d |
| mghs |
| d |
| mb2 |
| 2t2 |
| mb2 |
| 2t2 |
| 1 |
| t2 |
| ghs |
| b2d |
| 1 |
| t2 |
| ghs |
| b2d |
(2)多次改变光电门的位置,每次均令滑块自同一点(A点)下滑,测量相应的s与t值,结果如下表所示:
| 1 | 2 | 3 | 4 | 5 | |
| s/m | 0.60 | 0.80 | 1.00 | 1.20 | 1.40 |
| t/ms | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| /104s-2 | 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
2.40
2.40
×104m-1?s-2(保留3位有效数字).实验中,除了必须测量g、d和h的数值外,还应测量遮光片的宽度b
遮光片的宽度b
的数值,并用上述测量量表达k0=| gh |
| b2d |
| gh |
| b2d |
分析:本题的关键是滑块和砝码组成的系统机械能守恒,在求系统减少的重力势能时注意砝码的重力势能增加了mgs,滑块和砝码的速度大小相等,可求出系统增加的动能,然后根据机械能守恒可得出
与s的关系式,再讨论即可.
| 1 |
| t2 |
解答:解:(1)根据几何关系可得导轨倾角sinθ=
当滑块运动到B点时下降高度h′=s?sinθ=
,
滑块从A到B过程中系统重力势能减少量为△EP=mgh′=
滑块速度为v=
,所以系统动能增加量△EK=
mv2=
.
若机械能守恒应有△EP=△EK,将上式代入整理可得
=
(2)描点、连线如图所示,
在图中直线上取相距较远的两点,读出两点坐标,由k=可得:
k=2.40×104 m-1?s-2;
根据(1)的分析可知,要验证机械能守恒,需有:
=
,所以实验中,除了必须测量g、d和h的数值外,还应测量遮光片的宽度b的数值.
并用上述测量量表达k0=
.
故答案为:(1)
,
,
=
;(2)2.4)×104 m-1?s-2 (2.30~2.50)×104 m-1?s-2都同样给分.遮光片的宽度b,
.
| h |
| d |
当滑块运动到B点时下降高度h′=s?sinθ=
| sh |
| d |
滑块从A到B过程中系统重力势能减少量为△EP=mgh′=
| mghs |
| d |
滑块速度为v=
| b |
| t |
| 1 |
| 2 |
| mb2 |
| 2t2 |
若机械能守恒应有△EP=△EK,将上式代入整理可得
| 1 |
| t2 |
| ghs |
| b2d |
(2)描点、连线如图所示,

在图中直线上取相距较远的两点,读出两点坐标,由k=可得:
k=2.40×104 m-1?s-2;
根据(1)的分析可知,要验证机械能守恒,需有:
| 1 |
| t2 |
| ghs |
| b2d |
并用上述测量量表达k0=
| gh |
| b2d |
故答案为:(1)
| mghs |
| d |
| mb2 |
| 2t2 |
| 1 |
| t2 |
| ghs |
| b2d |
| gh |
| b2d |
点评:求解实验题的关键是正确利用物理规律列出方程,然后再求解即可,注意本实验属于滑块和砝码组成的系统的机械能守恒.

练习册系列答案
相关题目
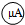 的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表
的刻度盘只标注了表示量程Ig=100μA的刻度线,尚未标注其他分刻度线,如图所2示.请用下列全部器材测量微安表 的内阻:
的内阻: :内阻Rg约为2kΩ
:内阻Rg约为2kΩ :量程250mV,最小分度5mV,内阻约为1kΩ
:量程250mV,最小分度5mV,内阻约为1kΩ 的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注).
的内阻Rg的实验电路原理图(原理图中的元①要用相应的英文字母标注). 的内阻Rg=
的内阻Rg=