题目内容
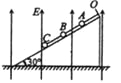
【题目】如图所示,三个可视为质点的金属小球A、B、C,质量分别为m、2m和3m,B球带负电,电荷量为﹣q,A、C不带电,不可伸长的绝缘细线将三球连接,最上边的细线连接在斜面顶端的O点,三球均处于场强大小为E的竖直向上的匀强电场中,三段细线均伸直,三个金属球均静止于倾角为30°的绝缘光滑斜面上,则下列说法正确的是
A. A、B球间的细线的张力为![]()
B. A、B球间的细线的张力可能为0
C. 将线OA剪断的瞬间,B、C间的细线张力![]()
D. 将线OA剪断的瞬间,A、B球间的细线张力![]()
【答案】AD
【解析】试题分析:静止时,先对三个球整体受力分析,则有TOA=(mg+2mg+3mg+Eq)sin30°,对A球进行受力分析,则有:TOA=TAB+mgsin30°,得TAB=(2mg+3mg+Eq)sin30°=![]() (5mg+Eq),故A正确,B错误;B球带负电,相当于在上述状态下给B球瞬间一个施加竖直向下的电场力qE,经过AB绳传递,qE对A、B球整体产生一个竖直向下的加速度
(5mg+Eq),故A正确,B错误;B球带负电,相当于在上述状态下给B球瞬间一个施加竖直向下的电场力qE,经过AB绳传递,qE对A、B球整体产生一个竖直向下的加速度![]() ,此时A、B球的加速度为
,此时A、B球的加速度为![]() >
>![]() g,C球以加速度
g,C球以加速度![]() g做匀加速运动,所以BC间绳子的作用力为零,以A球为研究对象可得A、B球间细线的拉力为
g做匀加速运动,所以BC间绳子的作用力为零,以A球为研究对象可得A、B球间细线的拉力为![]() ,故C错误,D正确.故选AD。
,故C错误,D正确.故选AD。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目