题目内容
18.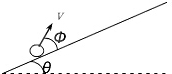 如图所示,倾角为θ的斜面光滑,自斜面上某处以速度v与斜面夹角为Φ的方向向斜面上抛出一质点(设质点与斜面间的碰撞是完全弹性的,即球入射方向与反射遵循光的反射定律),斜面足够长,要求质点最后仍能回到原出发点.问:Φ角应满足什么条件?
如图所示,倾角为θ的斜面光滑,自斜面上某处以速度v与斜面夹角为Φ的方向向斜面上抛出一质点(设质点与斜面间的碰撞是完全弹性的,即球入射方向与反射遵循光的反射定律),斜面足够长,要求质点最后仍能回到原出发点.问:Φ角应满足什么条件?
分析 整个过程中,质点只有重力做功,故机械能守恒,显然,若质点能回到原出发点,则它沿斜面向上的运动和向下的运动一定是相对称的,即质点沿斜面方向运动到其能达到的最高点后,沿原路返回.满足以上条件的有两种情况:一是质点最后一次与斜面相碰时,其速度方向刚好与斜面垂直,则其反射起来的速度与其碰前的速度大小相等方向相反;二是质点最后一次与斜面相碰后,反弹的速度沿竖直方向,然后再落后,“反演”此前的运动,也可以回到原出发点.根据以上两种情况进行分析.
解答  解:(1)建立如图所示的坐标系,设质点沿垂直斜面的方向以某一速度抛出,在质点再次与斜面相碰前,质点在空中运动的加速度分量分别为:
解:(1)建立如图所示的坐标系,设质点沿垂直斜面的方向以某一速度抛出,在质点再次与斜面相碰前,质点在空中运动的加速度分量分别为:
ax=gsinθ
ay=-gcosθ
在某一时刻t时,质点的速度两分量为:
vy=v0-gcosθt
vx=gsinθt
质点的位置坐标为:
x=$\frac{1}{2}$gsinθt2
y=v0t-$\frac{1}{2}$gcosθt2
由上式令y=0得质点由出发至第一次与斜面相碰所经历的时间为:
T=$\frac{2{v}_{0}}{gcosθ}$
此时质点的速度分量为:
vy=-v0;
vx=gsinθT
质点由斜面反弹起来时,其垂直于斜面方向的速度大小为v0,可见此后质点每两次与斜面相碰的时间间隔为T,则质点第n次与斜面相碰时的速度分量分别为
vy=-v0
vx=gsinθ•nT
令此时速度方向与斜面间的夹角为Φ,则有
tanΦ=|$\frac{{v}_{y}}{{v}_{x}}$|=$\frac{{v}_{0}}{ngsinθ-\frac{2{v}_{0}}{gcosθ}}$=$\frac{ctgθ}{2n}$(n=1,2---)
(2)设质点由空中自由下落到斜面上,与斜面相碰时速度为v0,仍在图中所示的坐标系中,由上分析可得:质点连续两次与斜面相碰的时间间隔为:
T=$\frac{2{v}_{0}cosθ}{gcosθ}$=$\frac{2{v}_{0}}{g}$;
此后,质点第n次与斜面相碰时其速度分量为:
vx=v0sinθ+gsinθ(n-1)T
vy=-v0cosθθ
由以上三式解得,质点第n次与斜面相碰时,速度方向与斜面间的夹角Φ满足:
tanΦ=|$\frac{{v}_{y}}{{v}_{x}}$|=$\frac{{v}_{0}ctgθ}{{v}_{0}+2{v}_{0}(n-1)}$=$\frac{ctgθ}{2n-1}$(n=1,2---)
(3)由以上分析可知,若将运动情况逆转,则依以上两问题中的结论可确定的Φ角方向抛出质点,则质点将沿原路返回;由以上分析可知,在斜面上抛出质点的速度方向与斜面的夹角只要满足tanΦ=$\frac{ctgθ}{k}$(k=1,2--)时,质点便能返回原出发点.
答:Φ角应满足条件为tanΦ=$\frac{ctgθ}{k}$(k=1,2--)
点评 本题考查运动的合成与分解与牛顿第二定律的应用,该题难度较大,为竞赛题目,对学生分析及应用数学规律求解物理问题的能力要求极高.

 快捷英语周周练系列答案
快捷英语周周练系列答案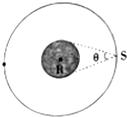 如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对于卫星S的张角为θ.地球视为质量分布均匀的球体,其表面重力加速度为g,引力常量为G.求:
如图所示,某卫星S绕地球做周期为T的匀速圆周运动,地球相对于卫星S的张角为θ.地球视为质量分布均匀的球体,其表面重力加速度为g,引力常量为G.求:(1)卫星S的速度大小;
(2)地球的第一宇宙速度.
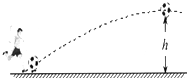 如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )
如图所示,运动员把静止的足球从水平地面踢出,足球在空中最高点的高度为h、速度为v.已知足球的质量为m,质量加速度为g,不计空气阻力.下列说法正确的是( )| A. | 运动员踢球时对足球做功$\frac{1}{2}$mv2 | |
| B. | 运动员踢球时对足球做功mgh+$\frac{1}{2}$mv2 | |
| C. | 足球上升过程克服重力做功mgh+$\frac{1}{2}$mv2 | |
| D. | 足球上升过程克服重力做功mgh |
| A. | 质点沿水平方向还是沿竖直方向振动 | |
| B. | 波沿水平方向还是沿竖直方向传播 | |
| C. | 质点的振动方向和波的传播方向是相互垂直还是平行 | |
| D. | 波传播距离的远近 |
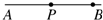 如图所示,AB是某点电荷电场中一条电场线,在电场线上P处自由释放一个负试探电荷时,它沿直线向B点处运动,对此现象下列判断正确的是( )
如图所示,AB是某点电荷电场中一条电场线,在电场线上P处自由释放一个负试探电荷时,它沿直线向B点处运动,对此现象下列判断正确的是( )| A. | 电荷向B做匀加速运动 | |
| B. | 电荷向B做加速度越来越小的运动 | |
| C. | 电荷向B做加速度越来越大的运动 | |
| D. | 电荷向B做加速运动,加速度的变化情况不能确定 |
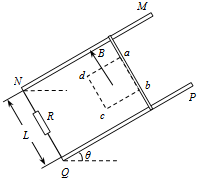 如图所示,间距为L,足够长的光滑金属导轨MN和PQ放在倾角为θ的斜面上,在N和Q之间连有一个阻值为R电阻.两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向垂直斜面向上的匀强磁场,磁感应强度为B.在导轨上放置一根与导轨垂直的金属杆,金属杆质量为m、电阻为r.金属杆从ab处无初速释放,运动过程中始终与导轨保持垂直且接触良好,金属杆离开磁场前已做匀速运动,不计导轨的电阻,重力加速度为g.求:
如图所示,间距为L,足够长的光滑金属导轨MN和PQ放在倾角为θ的斜面上,在N和Q之间连有一个阻值为R电阻.两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向垂直斜面向上的匀强磁场,磁感应强度为B.在导轨上放置一根与导轨垂直的金属杆,金属杆质量为m、电阻为r.金属杆从ab处无初速释放,运动过程中始终与导轨保持垂直且接触良好,金属杆离开磁场前已做匀速运动,不计导轨的电阻,重力加速度为g.求: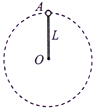 如图所示,长L=0.5m,质量可以忽略的杆,一端连接着一个质量为m=2kg的小球A,另一端可绕O点在竖直平面内做圆周运动.取g=10m/s2,在A以速率v=1m/s通过最高点时,小球A 对杆的作用力大小为16N,方向是竖直向下.
如图所示,长L=0.5m,质量可以忽略的杆,一端连接着一个质量为m=2kg的小球A,另一端可绕O点在竖直平面内做圆周运动.取g=10m/s2,在A以速率v=1m/s通过最高点时,小球A 对杆的作用力大小为16N,方向是竖直向下.