题目内容
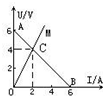 如图所示,图线AB是电路的路端电压随电流变化的关系图线.OM是同一电源向固定电阻R供电时,R两端的电压电变化的图线,点C为两图线的交点,则R的阻值
如图所示,图线AB是电路的路端电压随电流变化的关系图线.OM是同一电源向固定电阻R供电时,R两端的电压电变化的图线,点C为两图线的交点,则R的阻值2Ω
2Ω
,在交点C处表示电源的输出功率8W
8W
,在C点,电源内部消耗的电功率4W
4W
,电源的最大输出功率9W
9W
.分析:(1)根据伏安特性曲线OM的斜率求出电阻的阻值.
(2)交点C对应的电压和电流为电源输出电压和输出电流,根据P=UI求出电源的输出功率.
(3)根据电源路端电压和电流的变化关系图线求出电源的电动势和内阻,从而根据P=I2r求出电源内部消耗的功率.
(4)当外电阻等于内阻时,电源输出功率最大.
(2)交点C对应的电压和电流为电源输出电压和输出电流,根据P=UI求出电源的输出功率.
(3)根据电源路端电压和电流的变化关系图线求出电源的电动势和内阻,从而根据P=I2r求出电源内部消耗的功率.
(4)当外电阻等于内阻时,电源输出功率最大.
解答:解:
(1)OM是电阻的伏安特性曲线,其斜率等于电阻,则电阻 R=
=
Ω=2Ω;
(2)交点C对应的电压和电流,表示电源的工作状态,则电源的输出功率为PC出=UcIc=4×2(W)=8(W)
(3)由图可知,电源的电动势 E=6V,根据闭合电路欧姆定律,可得电源的内阻 r=
=
=1Ω
在C点电源内部消耗的功率为 PC内=Ic2?r=22×1(W)=4W
(4)电源的最大输出功率Pm,是在外电阻的阻值恰等于电源内电阻时达到的.
Pm=
=
(W)=9W
故答案为:2Ω,8W,4W,9W.
(1)OM是电阻的伏安特性曲线,其斜率等于电阻,则电阻 R=
| U |
| I |
| 4 |
| 2 |
(2)交点C对应的电压和电流,表示电源的工作状态,则电源的输出功率为PC出=UcIc=4×2(W)=8(W)
(3)由图可知,电源的电动势 E=6V,根据闭合电路欧姆定律,可得电源的内阻 r=
| E-U |
| I |
| 6-4 |
| 2 |
在C点电源内部消耗的功率为 PC内=Ic2?r=22×1(W)=4W
(4)电源的最大输出功率Pm,是在外电阻的阻值恰等于电源内电阻时达到的.
Pm=
| E2 |
| 4r |
| 62 |
| 4×1 |
故答案为:2Ω,8W,4W,9W.
点评:对于图线关键要根据物理规律,从数学角度来理解其物理意义.本题要抓住图线的斜率、交点的意义来理解图象的意义.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
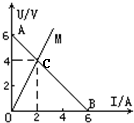 如图所示,图线AB是电路的路端电压随电流变化的关系图线.OM是同一电源向固定电阻R供电时,R两端的电压电变化的图线,由图求:
如图所示,图线AB是电路的路端电压随电流变化的关系图线.OM是同一电源向固定电阻R供电时,R两端的电压电变化的图线,由图求: 如图所示,图线AB是某电源的路端电压随电流变化的关系图线;OM是同一电源向固定电阻R供电时,R两端的电压随电流变化的图线,由图可知( )
如图所示,图线AB是某电源的路端电压随电流变化的关系图线;OM是同一电源向固定电阻R供电时,R两端的电压随电流变化的图线,由图可知( )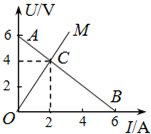 如图所示,图线AB是某电源的路端电压随电流变化的关系图线;OM是固定电阻R两端的电压随电流变化的图线,由图可知( )
如图所示,图线AB是某电源的路端电压随电流变化的关系图线;OM是固定电阻R两端的电压随电流变化的图线,由图可知( )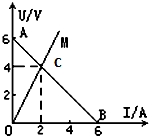 如图所示,图线AB是某电源的路端电压随电流变化的关系图线.OM是某固定电阻R1的电流随两端电压变化的图线,点C为两图线的交点,由图象可知:电源电动势E=
如图所示,图线AB是某电源的路端电压随电流变化的关系图线.OM是某固定电阻R1的电流随两端电压变化的图线,点C为两图线的交点,由图象可知:电源电动势E=