题目内容
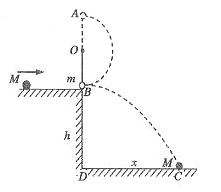
如图所示,O点为固定转轴,把一个长度为L的细绳上端固定在O点,细绳下端系一个质量为m的小摆球,当小摆球处于静止状态时恰好与平台的右端点B点接触,但无压力。一个质量为M的小钢球沿着光滑的平台自左向右运动到B点时与静止的小摆球m发生正碰,碰撞后摆球在绳的约束下作圆周运动,且恰好能够经过最高点A,而小钢球M做平抛运动落在水平地面上的C点。测得B、C两点间的水平距离DC=x,平台的高度为h,不计空气阻力,本地的重力加速度为g,请计算:
(1)碰撞后小钢球M做平抛运动的初速度大小;
(2)小球m经过最高点A时的动能;
(3)碰撞前小钢球M在平台上向右运动的速度大小。
(1)碰撞后小钢球M做平抛运动的初速度大小;
(2)小球m经过最高点A时的动能;
(3)碰撞前小钢球M在平台上向右运动的速度大小。

(1) x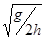 (2)
(2)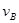 =
=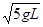 (3)v2=x
(3)v2=x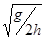 +
+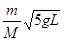
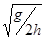 (2)
(2)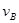 =
=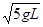 (3)v2=x
(3)v2=x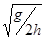 +
+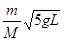
(1)碰后小钢球做平抛运动 x=v1t ,,,,,,,,,,,,,,,,,,,,,,,,,① (1分)
h=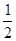 gt2 ,,,,,,,,,,,,,,,,,,,,,,,,,,② (1分)
gt2 ,,,,,,,,,,,,,,,,,,,,,,,,,,② (1分)
联合解出 v1=x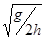 ,,,,,,,,,,,,,③ (2分)
,,,,,,,,,,,,,③ (2分)
(2)小球m恰能过最点 有 mg=m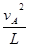 ,,,,,,,,,,,④ (2分)
,,,,,,,,,,,④ (2分)
所以 Ek=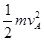 =
=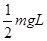 ,,,,,,,,,⑤ (1分)
,,,,,,,,,⑤ (1分)
从B到A由机械能守恒定律: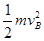 =mg2L+
=mg2L+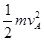 ,,,,,,,,,⑥(2分)
,,,,,,,,,⑥(2分)
解得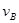 =
=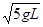 ,,,,,,,,,,,,⑦ (2分)
,,,,,,,,,,,,⑦ (2分)
(3)设M向右运动速度为v2 由碰撞时动量守恒:有 Mv2=Mv1+mvB ,,,,,⑧(2分)
联合解得 v2=x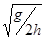 +
+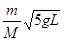 ,,,,,,,,,,,,,⑨ (3分)
,,,,,,,,,,,,,⑨ (3分)
h=
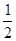 gt2 ,,,,,,,,,,,,,,,,,,,,,,,,,,② (1分)
gt2 ,,,,,,,,,,,,,,,,,,,,,,,,,,② (1分)联合解出 v1=x
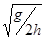 ,,,,,,,,,,,,,③ (2分)
,,,,,,,,,,,,,③ (2分)(2)小球m恰能过最点 有 mg=m
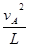 ,,,,,,,,,,,④ (2分)
,,,,,,,,,,,④ (2分)所以 Ek=
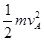 =
=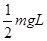 ,,,,,,,,,⑤ (1分)
,,,,,,,,,⑤ (1分)从B到A由机械能守恒定律:
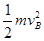 =mg2L+
=mg2L+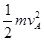 ,,,,,,,,,⑥(2分)
,,,,,,,,,⑥(2分)解得
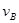 =
=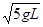 ,,,,,,,,,,,,⑦ (2分)
,,,,,,,,,,,,⑦ (2分)(3)设M向右运动速度为v2 由碰撞时动量守恒:有 Mv2=Mv1+mvB ,,,,,⑧(2分)
联合解得 v2=x
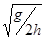 +
+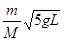 ,,,,,,,,,,,,,⑨ (3分)
,,,,,,,,,,,,,⑨ (3分)
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 (22分)整个装置图如图所示,在光滑绝缘水平面上固定一竖直的表面光滑的挡板,ABCD为挡板与水平面的交线,其中ABC为直线,CD为半径R=4.0 m的圆弧,C点为AC直线与CD圆弧的切点。整个装置置于真空中两有界的与水平面平行的匀强电场中,MN为两电场的分界面与水平面的交线,且MN垂直于AB,在MN的左侧有一沿AB方向场强大小为E1=5.0×105 V/m的匀强电场,在MN的右侧有一沿MN方向场强大小为E2=1.0×107 V/m的匀强电场。质量m2=4.0×10-2 kg的不带电金属小球静置于C点,电量为q=+2.0×10-6 C、质量为m1=1.0×10-2 kg的小球Q自A点静止释放(P、Q两金属球的大小完全相同)。已知AB=0.5 m,BC=1.20 m,cos10°=0.985,=π,简谐振动的周期公式为T=2π,式中m为振子的质量,k是回复力与位移大小的比值且为常数。试求P、Q两球在距A点多远处第二次相碰(不计碰撞时机械能损失和电荷间的相互作用力,结果取三位有效数字)。
(22分)整个装置图如图所示,在光滑绝缘水平面上固定一竖直的表面光滑的挡板,ABCD为挡板与水平面的交线,其中ABC为直线,CD为半径R=4.0 m的圆弧,C点为AC直线与CD圆弧的切点。整个装置置于真空中两有界的与水平面平行的匀强电场中,MN为两电场的分界面与水平面的交线,且MN垂直于AB,在MN的左侧有一沿AB方向场强大小为E1=5.0×105 V/m的匀强电场,在MN的右侧有一沿MN方向场强大小为E2=1.0×107 V/m的匀强电场。质量m2=4.0×10-2 kg的不带电金属小球静置于C点,电量为q=+2.0×10-6 C、质量为m1=1.0×10-2 kg的小球Q自A点静止释放(P、Q两金属球的大小完全相同)。已知AB=0.5 m,BC=1.20 m,cos10°=0.985,=π,简谐振动的周期公式为T=2π,式中m为振子的质量,k是回复力与位移大小的比值且为常数。试求P、Q两球在距A点多远处第二次相碰(不计碰撞时机械能损失和电荷间的相互作用力,结果取三位有效数字)。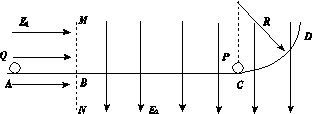

 跃迁到n=4的能级。求碰撞后一个电子和一个受激氢原子的总动能。已知电子的质量me与氢原子的质量mH之比为
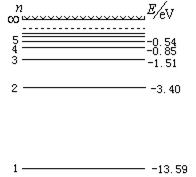
跃迁到n=4的能级。求碰撞后一个电子和一个受激氢原子的总动能。已知电子的质量me与氢原子的质量mH之比为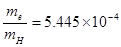 。
。
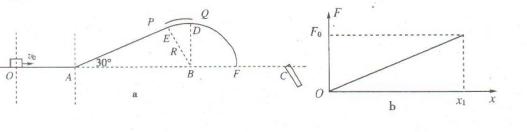
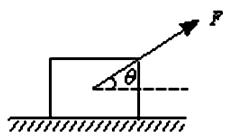
 ,EDF是圆心在B点,半径为R的光滑圆弧,D点是最高点,ED圆弧上方有一个高度与滑块相近的光滑圆弧形挡板PQ,轨道上的A、E两点理想连接,使滑块经过这两点时不损失机械能,且AE⊥EB可视为质点的滑块,质量为m,以v0的初速度从O点进入OA直轨道,滑块在OA轨道运动时,受到水平向右的动力作用,它的大小随滑块与O点的距离变化,如图b所示,图中F0=mg滑块经A点滑上斜轨道,到达轨道最高点D时恰好对轨道和挡板都无压力,此时立刻撤除圆弧形挡板PQ滑块经D点后能无碰撞地进入一个特殊的漏斗C,漏斗C能将滑块以进入时的速率反向弹出,求:
,EDF是圆心在B点,半径为R的光滑圆弧,D点是最高点,ED圆弧上方有一个高度与滑块相近的光滑圆弧形挡板PQ,轨道上的A、E两点理想连接,使滑块经过这两点时不损失机械能,且AE⊥EB可视为质点的滑块,质量为m,以v0的初速度从O点进入OA直轨道,滑块在OA轨道运动时,受到水平向右的动力作用,它的大小随滑块与O点的距离变化,如图b所示,图中F0=mg滑块经A点滑上斜轨道,到达轨道最高点D时恰好对轨道和挡板都无压力,此时立刻撤除圆弧形挡板PQ滑块经D点后能无碰撞地进入一个特殊的漏斗C,漏斗C能将滑块以进入时的速率反向弹出,求: