Question

【题目】在平面直角坐标系中，若点P（x，y）的坐标x，y均为整数，对称点P为格点．若一个多边形的顶点全是格点，则称该多边形为格点多边形．格点多边形的面积记为S，其内部的格点数记为N．边界上的格点数记为L．例如图中△ABC是格点三角形，对应的S=1，N=0，L=4．

（1）图中格点四边形DEFG对应的S，N，L分别是 ．
（2）已知格点多边形的面积可表示为S=aN+bL+c，其中a，b，c为常数，若某格点多边形对应的N=17，L=10，则S=（用数值作答）．

Answer 1

【答案】
（1）3，1，6
（2）79
【解析】解：（1）观察图形，可得四边形的面积为S= ×2×1+ ×2×2=3，
四边形内的点为N=1，边界上的点为L=6；（2）不妨设某个格点四边形由两个小正方形组成，此时S=2，N=0，L=6；
∵格点多边形的面积S=aN+bL+c，
∴结合图中的格点三角形ABC及格点四边形DEFG可得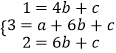
，
解得 ，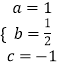
∴S=N+ L﹣1；
将N=71，L=18代入可得S=71+ ×18﹣1=79．
所以答案是：（1）3，1，6；（2）79．
【考点精析】根据题目的已知条件，利用向量的物理背景与概念和平面向量的基本定理及其意义的相关知识可以得到问题的答案，需要掌握了解四种常见向量：力、位移、速度、加速度；既有大小又有方向的量叫做向量；如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使．